Question

How do you use a graphing calculator to find the limit of the sequence ${a_n} = {\left( {\dfrac{1}{2}} \right)^n}$ ?

Answer 1

Hint : Here the given question based on geometric series. We have to plot a graph of the given function of the series. Firstly, we have to make a sequence of series by giving a n values, where n belongs to integers i.e., $n \in I$ . After that plot a graph by taking n values in x-axis and ${a_n}$ values in y-axis.

Complete step by step solution:
A geometric series is also termed as the geometric progression. It is a series formed by multiplying the first term by a fixed value to get the second term. This process is continued until we get a required number of terms in the series. Such a progression increases in a specific way and hence giving a geometric progression.
Consider, the given limit of the sequence:
$\Rightarrow {a_n} = {\left( {\dfrac{1}{2}} \right)^n}$ where $n \in I$ .
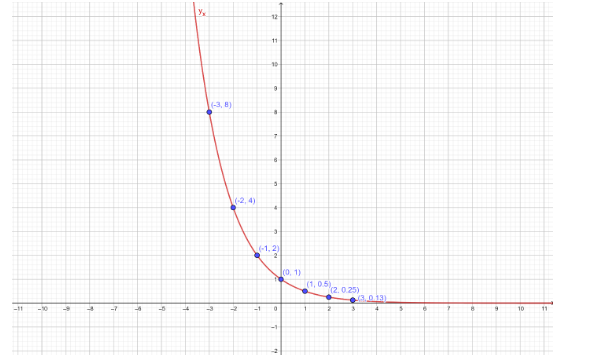
Now giving the n values … -3, -2, -1, 0, 1, 2, 3, … to the above equation simultaneously we get the values of ${a_n}$ .
Now put $n = - 3$ , then
$\Rightarrow {a_{ - 3}} = {\left( {\dfrac{1}{2}} \right)^{ - 3}}$
$\Rightarrow {a_{ - 3}} = \dfrac{1}{{{2^{ - 3}}}}$
$\Rightarrow {a_{ - 3}} = {2^3} = 8$
Put $n = - 2$ , then
$\Rightarrow {a_{ - 2}} = {\left( {\dfrac{1}{2}} \right)^{ - 2}}$
$\Rightarrow {a_{ - 2}} = {2^2} = 4$
Put $n = - 1$ , then
$\Rightarrow {a_{ - 1}} = {\left( {\dfrac{1}{2}} \right)^{ - 1}}$
$\Rightarrow {a_{ - 1}} = {2^1} = 2$
Put $n = 0$ , then
$\Rightarrow {a_0} = {\left( {\dfrac{1}{2}} \right)^0}$
$\Rightarrow {a_0} = 1$
Put $n = 1$ , then
$\Rightarrow {a_1} = {\left( {\dfrac{1}{2}} \right)^1}$
$\Rightarrow {a_1} = 0.5$
Put $n = 2$ , then
$\Rightarrow {a_2} = {\left( {\dfrac{1}{2}} \right)^2}$
$\Rightarrow {a_2} = \dfrac{1}{{{2^2}}} = \dfrac{1}{4}$
$\Rightarrow {a_2} = 0.25$
Put $n = 3$ , then
$\Rightarrow {a_3} = {\left( {\dfrac{1}{2}} \right)^3}$
$\Rightarrow {a_3} = \dfrac{1}{{{2^3}}} = \dfrac{1}{8}$
$\Rightarrow {a_3} = 0.125$
And so on…
Hence the sequence ${a_n}$ as written as:
$\Rightarrow {a_n} = \cdot \cdot \cdot ,8,4,2,1,0.5,0.25,0.125, \cdot \cdot \cdot$
Now, we can plot the graph of ${a_n} = {\left( {\dfrac{1}{2}} \right)^n}$ , by taking n values in x-axis and ${a_n}$ values in y-axis.

Note: The question is belonging to the concept of graph. To plot a graph first we have to choose which one is x-axis and y-axis. Or by choosing the value of x we can determine the value of y and then plotting the graphs for these points we obtain the result.