Question

How do you to prove $\dfrac{\tan A+\tan B}{1-\tan A\tan B}=\dfrac{\cot A+\cot B}{1-\cot A\cot B}$ ?

Answer 1

We recall tangent and cotangent of an angle as a ratio right angled triangle. We recall that tangent and cotangent ratios are reciprocal to each other to have $\tan \theta =\dfrac{1}{\cot \theta }$. We use this relation and replace tangents at left hand side by co-tangents. We proceed to the right hand side.

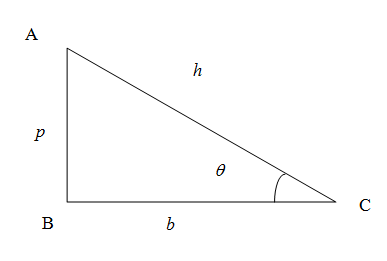
Complete step by step answer:
We know that in right angled triangle the side opposite to right angled triangle is called hypotenuse denoted as $h$, the vertical side is called perpendicular denoted as $p$ and the horizontal side is called the base denoted as $b$.$$$$
The tangent of the angle is the ratio of opposite side to the adjacent side (excluding hypotenuse) . So we have tangent of the angle $\theta$
$\tan \theta =\dfrac{p}{b}$
The co-tangent tangent of the angle is the ratio of the adjacent side (excluding hypotenuse) to the opposite side too . So we have tangent of the angle $\theta$
$\cot \theta =\dfrac{b}{p}$
We see that

& \tan \theta \times \cot \theta =\dfrac{p}{b}\times \dfrac{b}{p}=1 \\\ & \Rightarrow \tan \theta =\dfrac{1}{\cot \theta } \\\ \end{aligned}$$ The above relation is called reciprocal relation between tangent and cotangent. We are asked to prove the following statement $$\dfrac{\tan A+\tan B}{1-\tan A\tan B}=\dfrac{\cot A+\cot B}{1-\cot A\cot B}$$ Let us begin from the left hand side by converting the tangents at left hand side to cotangents using $\tan \theta =\dfrac{1}{\cot \theta }$ for $\theta =A,B$ to have; $$\begin{aligned} & \dfrac{\tan A+\tan B}{1-\tan A\tan B} \\\ & \Rightarrow \dfrac{\dfrac{1}{\cot A}+\dfrac{1}{\cot B}}{1-\dfrac{1}{\cot A}\cdot \dfrac{1}{\cot B}} \\\ & \Rightarrow \dfrac{\dfrac{1}{\cot A}+\dfrac{1}{\cot B}}{1-\dfrac{1}{\cot A\cot B}} \\\ \end{aligned}$$ We add the cotangents terms in the numerator and subtract in the denominator to have $$\Rightarrow \dfrac{\dfrac{\cot B+\cot A}{\cot A\cot B}}{\dfrac{\cot A\cot B-1}{\cot A\cot B}}$$ We cancel out $\cot A\cot B$ from the numerator and denominator to have; $$\Rightarrow \dfrac{\cot A+\cot B}{\cot A\cot B-1}$$ The above expression is the expression at the right hand side of the statement. Hence the required statement is proved. **Note:** We can alternatively prove beginning fro right side by converting cotangents to tangents using $\cot \theta =\dfrac{1}{\tan \theta }$ for $\theta =A,B$. The expression $\dfrac{\tan A+\tan B}{1-\tan A\tan B}$ is the expression for tangent sum of angles $\tan \left( A+B \right)$. The given statement fails for $A,B={{90}^{\circ }}$ since tangent is undefined for ${{90}^{\circ }}$ and for $A,B\ne {{0}^{\circ }}$ since cotangent is undefined for ${{0}^{\circ }}$.