Question

How do you tell whether the graph opens up or down, find the vertex, and find the axis of symmetry of $y=-{{\left( x+1 \right)}^{2}}+2$?

Answer 1

First try to find the nature of the curve or equation. Then convert the standard form of equation of parabola to that of extended form as required. Consider all parameters to find the required solution.

Complete step by step answer:
We know the standard equation of parabola is $y={{x}^{2}}$ which opens up, vertex is at $\left( 0,0 \right)$ and the parabola is symmetric about ‘x’- axis.
It can be extended as $\left( y-k \right)=-{{\left( x-h \right)}^{2}}+c$ where the ‘$-$’ sign indicates that the parabola opens down and ‘c’ is any constant, vertex is at $\left( h,k+c \right)$ and the parabola is symmetric about ‘x’-axis.
Now coming back to our equation $y=-{{\left( x+1 \right)}^{2}}+2$ and comparing with the standard form, we get $h=-1$, $k=0$ and $c=2$
The parabola opens down as there is a ‘$-$’ sign.
The vertex is at $\left( h,k+c \right)=\left( -1,0+2 \right)=\left( -1,2 \right)$
The axis of symmetry is ‘x’-axis.
The parabola can be graphed as follows

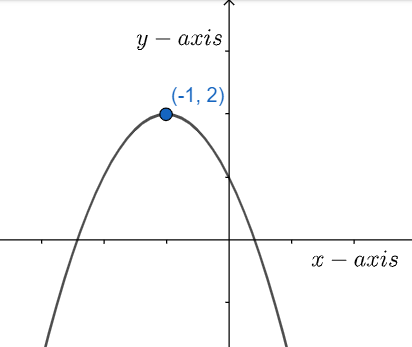
Note: Finding the nature of the curve should be the first approach. The given equation should be compared with the extended form of equation of parabola to get all the parameters. The constant on the right side of the equation should be added to the ‘y’- coordinate of the vertex according to the extended form. As the line of vertex is parallel to ‘x’- axis so the axis of symmetry should also be ‘x’- axis.