Question

How do you state the coordinates of the vertex of the parabola whose equation is $y=3{{\left( x-2 \right)}^{2}}+5$?

Answer 1

The equation of the parabola, which is given in the above question as $y=3{{\left( x-2 \right)}^{2}}+5$, is linear in y and quadratic in x. This means that the axis of the parabola is vertical. The vertex of a vertical parabola is the point lying on the parabola where its slope is equal to zero. Therefore, for determining the vertex of the given parabola, we need to differentiate its equation with respect to x. Then on equating the differentiated expression to zero, we will obtain the abscissa of the vertex. Substituting the value of the abscissa back into the given equation, we will get the ordinate of the vertex, and hence the coordinates of the vertex will be determined.

Complete step by step solution:
The equation of the parabola given in the above question is
$\Rightarrow y=3{{\left( x-2 \right)}^{2}}+5.......\left( i \right)$
We can see that the above equation is linear in y and quadratic in x. Therefore, the axis of the parabola must be vertical. Therefore, at the vertex, the slope or the derivative must be equal to zero. Therefore, for the vertex we can write
$\Rightarrow \dfrac{dy}{dx}=0$
Putting (i) in the above equation, we get
$\begin{aligned} & \Rightarrow \dfrac{d\left[ 3{{\left( x-2 \right)}^{2}}+5 \right]}{dx}=0 \\\ & \Rightarrow 3\times 2\left( x-2 \right)\times 1+0=0 \\\ & \Rightarrow 6\left( x-2 \right)=0 \\\ & \Rightarrow x-2=0 \\\ & \Rightarrow x=2 \\\ \end{aligned}$
Therefore, the abscissa of the vertex is equal to $2$. Substituting $x=2$ in the equation (i) we get
$\begin{aligned} & \Rightarrow y=3{{\left( 2-2 \right)}^{2}}+5 \\\ & \Rightarrow y=3{{\left( 0 \right)}^{2}}+5 \\\ & \Rightarrow y=5 \\\ \end{aligned}$
Therefore, the ordinate of the vertex is equal to $5$.
Hence, the coordinates of the vertex are $\left( 2,5 \right)$.
We can observe this in the below graph.

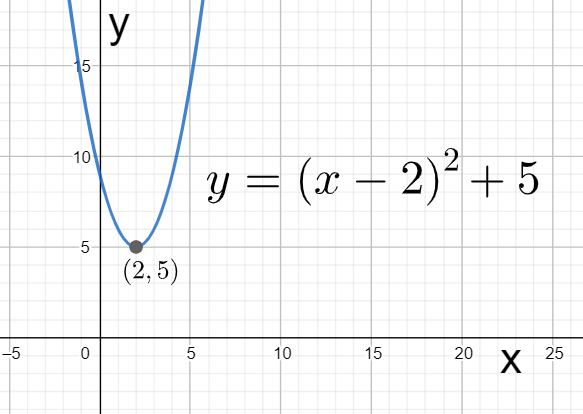
Note: We can also determine the coordinates of the vertex of the parabola by writing the given equation in the standard form of $\left( y-k \right)=a{{\left( x-h \right)}^{2}}$. For this we can subtract $5$ from both the sides of the given equation to get $\left( y-5 \right)=3{{\left( x-2 \right)}^{2}}$. From here we can directly state the coordinates of the vertex as $\left( 2,5 \right)$.