Solveeit Logo
Login

Question

Question: How do you state the coordinates of the vertex of the parabola whose equation is : \(y = 3{\left( {x...

How do you state the coordinates of the vertex of the parabola whose equation is : y=3(x−2)2+5y = 3{\left( {x - 2} \right)^2} + 5?

Explanation

Solution

This problem deals with the conic sections. A conic section is a curve obtained as the intersection of the surface of a cone with a plane. There are three such types of conic sections which are, the parabola, the hyperbola and the ellipse. This problem is regarding one of those conic sections, which is a parabola. The general form of an equation of a parabola is given by x2=4ay{x^2} = 4ay.

Complete step-by-step answer:
Now consider the given parabola equation y=3(x−2)2+5y = 3{\left( {x - 2} \right)^2} + 5.
Simplifying the given parabola equation as given below:
⇒y=3x2−12x+17\Rightarrow y = 3{x^2} - 12x + 17
If the parabola is given by y=ax2+bx+cy = a{x^2} + bx + c, then the x-coordinate of the vertex is given by:
⇒x=−b2a\Rightarrow x = \dfrac{{ - b}}{{2a}}
Here in the given parabola equation y=3x2−12x+17y = 3{x^2} - 12x + 17, here a=3,b=−12a = 3,b = - 12 and c=17c = 17.
Now finding the x-coordinate of the vertex:
⇒x=−(−12)2(3)\Rightarrow x = \dfrac{{ - \left( { - 12} \right)}}{{2\left( 3 \right)}}
⇒x=2\Rightarrow x = 2
Now to get the y-coordinate of the vertex of the parabola, substitute the value of x=2x = 2, in the parabola equation, as shown below:
⇒y=3(2)2−12(2)+17\Rightarrow y = 3{\left( 2 \right)^2} - 12\left( 2 \right) + 17
⇒y=3(4)−24+17\Rightarrow y = 3\left( 4 \right) - 24 + 17
Simplifying the above equation, as given below:
⇒y=12−7\Rightarrow y = 12 - 7
∴y=5\therefore y = 5
So the vertex of the parabola y=3x2−12x+17y = 3{x^2} - 12x + 17 is A, which is given by:
⇒A=(2,5)\Rightarrow A = \left( {2,5} \right)
This parabola has its axis parallel to y-axis.
The graph of the given parabola is shown below:

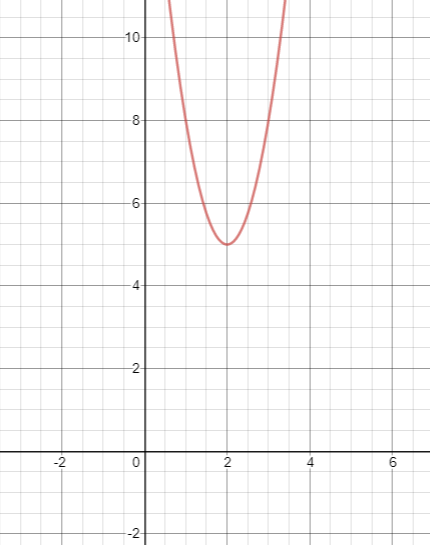
Final answer: The vertex of the parabola is (2,5)\left( {2,5} \right).

Note:
Please note that if the given parabola isx2=4ay{x^2} = 4ay, then the vertex of this parabola is the origin (0,0)\left( {0,0} \right), and there is no intercept for this parabola as there are no terms of x or y. If the equation of the parabola includes any terms of linear x or y, then the vertex of the parabola is not the origin, the vertex has to be found by simplifying it into its particular standard form.