Question

How do you solve $y=\dfrac{x}{3}$ and $y=\dfrac{x}{3}-2$ ?

Answer 1

There are few general methods to solve two-line equations. There is a substitution method. There is an elimination method. Substitution method can be lengthy sometimes so let’s try using the elimination method here.

Complete step by step answer:
Let’s make use of the slope intercept equation of a line.
The general slope intercept equation of a line is $y=mx+c$ where $m$ is the slope of the given line and $c$ is the constant or the value which gives the length of the intercept that the line is cutting on $y$- axis.
When the slopes of two lines i.e., the values of $m$ is the same for both the lines, it indicates that the two lines are parallel and never intersect each other at any point.
When we are solving any number of line equations, it is nothing but finding out the point of intersection of all the lines. Let it be a family of lines or just two lines. But since in the question we have $y=\dfrac{x}{3}$ and $y=\dfrac{x}{3}-2$ whose slopes are $\dfrac{1}{3}$ .
So, these two lines are parallel and can never meet. Hence, we cannot solve these two lines.
Graph for reference:

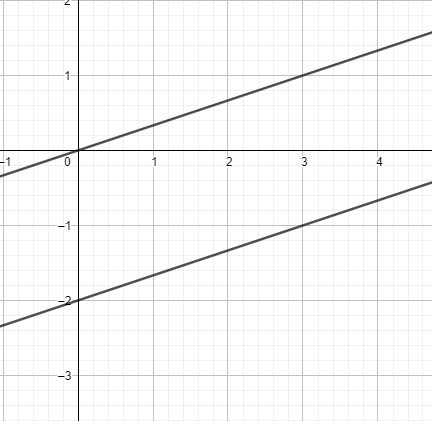
The grey line represents $y=\dfrac{x}{3}$ and the blue line represents $y=\dfrac{x}{3}-2$ .

Note:
Please be careful while solving. Not all equations are solve-able. Keep all the general equations of the lines at your finger- tips to solve the problem and come to a conclusion quickly. We can also solve this question by comparing the ratios of the coefficient of $x$, $y$, and the constants.