Question

How do you solve $x – 3 < 3x – 7$ ?

Answer 1

In this question, we need to solve the given inequality equation $x – 3 < 3x – 7$ . Since the given expression is a linear inequality in one variable , it will have only one solution. We can find the value of $x$ by performing simple mathematical simplification with mathematical operations. First, we need to subtract $3x$ on both sides. Then we have to take the variable terms to one side of the inequality, and the constant terms to the other side. Thus on further simplifying, we can find $x$. Usually, Inequalities do not provide a fixed value as a solution; it gives a range. All the values in this range hold the inequality. With the value of $x$, we can find the range of the inequality.

Complete step by step answer:
Given, $x - 3 < 3x - 7$
Here we need to solve the given inequality. The given expression is a linear inequality with one unknown .
Now on subtracting both sides by $3x$ ,
We get,
$\Rightarrow \ x - 3 - 3x < 3x - 3x - 7$
On simplifying ,
We get,
$\Rightarrow \ - 2x - 3 < \- 7$
Now, We have to keep the variable term at one side of the inequality, and move the constant terms to the other side.
We get,
$\Rightarrow \ - 2x < \- 7 + 3$
On simplifying,
We get,
$\Rightarrow \ - 2x < \- 4$
On dividing both sides by $- 2$ ,
We get,
$\Rightarrow \ x > \dfrac{- 4}{- 2}$
When dividing or multiplying by a negative number, we always change the inequality sign.
Thus on simplifying,
We get,
$\Rightarrow \ x > 2$
Here we get the range of $x$ is greater than $2$ which implies that the given quantity can have any possible value above $2$ .
Thus the range of $x$ can be written as $(2,\ \infty)$ here open bracket ``( )'' is indicating that the value written in the bracket is not for the quantity $x$ but the very next closed value after $2$ is the value of $x$ , and since infinity is not known so we always provide an open bracket for infinity.

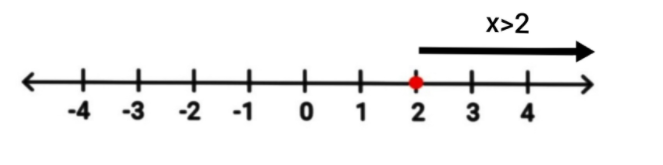
The inequality $x – 3 < 3x – 7$ is $x > 2$ and the range of $x$ is $(2,\ \infty)$.

Note: An inequality is nothing but a relation which makes a non-equal comparison between two numbers or other mathematical expressions and it is used most often to compare two numbers on the number line by their size. Mathematically, the arithmetic symbols, $<$ is known as less than symbol, $>$ as greater than symbol and $=$ is known as the equal to symbol. We may make mistakes in assigning the correct symbol, which may lead to wrong solutions. We need to know that the linear inequalities in one variable will have only one solution.