Question

How do you solve ${x^2} + 5 = 0$ by graphing?

Answer 1

To graph a solution, determine the variable from the given equation to graph and there should be points to graph the coordinates in rectangular coordinate system, hence to solve an equation graphically, draw the graph for each side, of the equation and see where the curves cross, and also see the points where it touches.

Complete step by step solution:
Given,
${x^2} + 5 = 0$
This question is basically asking if the lines $y = {x^2} + 5$ and $y = 0$ intersect at any points.
Hence, graphing each side of the equation we get:
$\Rightarrow y = {x^2} + 5$
$\Rightarrow y = 0$, we get the solution of the graph i.e., ${x^2} + 5 = 0$.

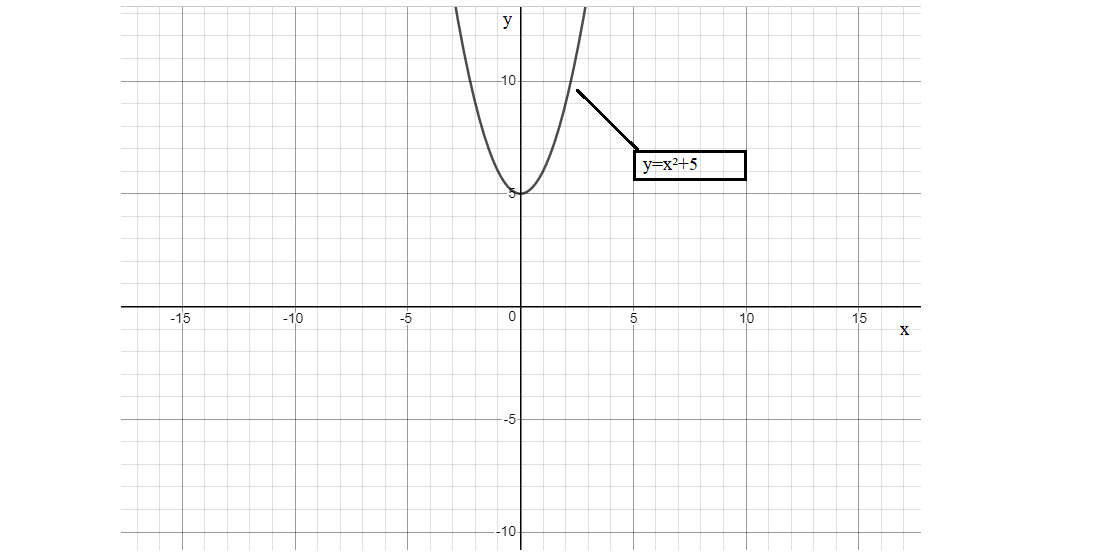
Above is the graph $y = {x^2} =-5$. Now, you see that the graph does not intersect with y=0 or the x-axis at any point. Therefore, the answer has no solution.

Additional information:
A system of linear equations contains two or more equations. The solution of such a system is the ordered pair that is a solution to both equations. To solve a system of linear equations graphically we graph both equations in the same coordinate system. Graph the first equation the graph the second equation on the same rectangular coordinate system. Determine whether the lines intersect, are parallel, or are the same line.

Note: We can also plot the graph using intercepts i.e., solving for x and y-intercept of the given equation, by putting x=0 and solve for y and y=0 an solve for x. We must know that another way to graph the solution is of solving a quadratic equation graphically. The roots of a quadratic equation are the x-intercepts of the graph then graph the equation of the points obtained.