Solveeit Logo
Login

Question

Question: How do you solve \({{x}^{2}}+4x+4\ge 9\) using a sign chart?...

How do you solve x2+4x+4≥9{{x}^{2}}+4x+4\ge 9 using a sign chart?

Explanation

Solution

We are given an inequality as x2+4x+4≥9{{x}^{2}}+4x+4\ge 9. We will learn about the type of this inequality and we will then transform it by making the right side as zero. We will use the middle term split method to simplify our terms into linear factors. Then we will use a sign chart to check for the region that should satisfy the inequality.

Complete step-by-step solution:
We are given an inequality as x2+4x+4≥9{{x}^{2}}+4x+4\ge 9. We can see that it has the highest power as 2, so it is a quadratic inequality. We will first transform and change the right side to 0. We will subtract 9 on both sides, so we get,
x2+4x+4−9≥9−9{{x}^{2}}+4x+4-9\ge 9-9
Simplifying we get,
⇒x2+4x−5≥0………(i)\Rightarrow {{x}^{2}}+4x-5\ge 0\ldots \ldots \ldots \left( i \right)
Now, we have a quadratic equation on the left. We will use the middle term split method to factor our inequality. In this method, we look for the numbers whose sum or difference is the same as the middle term, while the product is the same as the product of the coefficient of x2{{x}^{2}} and the constant term. Now as we have the equation as x2+4x−5{{x}^{2}}+4x-5, we can see that we have two numbers 5 and -1.
Product of 5×(−1)=−55\times \left( -1 \right)=-5 [same as the product of 1×(−5)=−51\times \left( -5 \right)=-5]
The sum is 5+(−1)=5−1=45+\left( -1 \right)=5-1=4 [same as the middle term]
So, we use this to split the idle term. So, we get,
x2+4x−5 ⇒x2+(5−1)x−5 ⇒x2+5x−x−5 \begin{aligned} & {{x}^{2}}+4x-5 \\\ & \Rightarrow {{x}^{2}}+\left( 5-1 \right)x-5 \\\ & \Rightarrow {{x}^{2}}+5x-x-5 \\\ \end{aligned}
Taking the common in the first two and last two terms, we get,
⇒x(x+5)−1(x+5)\Rightarrow x\left( x+5 \right)-1\left( x+5 \right)
As x+5x+5 is common, so, we get,
⇒(x−1)(x+5)\Rightarrow \left( x-1 \right)\left( x+5 \right)
So, we get,
⇒x2+4x−5=(x−1)(x+5)\Rightarrow {{x}^{2}}+4x-5=\left( x-1 \right)\left( x+5 \right)
Using this in equation (i), we get,
⇒(x−1)(x+5)≥0\Rightarrow \left( x-1 \right)\left( x+5 \right)\ge 0
Now, we consider this as equal and solve for zero. So, we have,
(x−1)(x+5)=0 ⇒x−1=0 or x+5=0 \begin{aligned} & \left( x-1 \right)\left( x+5 \right)=0 \\\ & \Rightarrow x-1=0\text{ or }x+5=0 \\\ \end{aligned}
Simplifying we get,
x=1 or x=−5x=1\text{ or }x=-5
Now we put this value of xx on the number line and ten we will look for the values. As we have (x−1)(x+5)≥0\left( x-1 \right)\left( x+5 \right)\ge 0, so we will look for which point is positive. We mark x=1 and x=−5x=1\text{ and }x=-5.

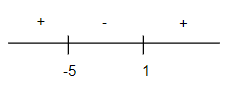
We see from the sign chart that the value is positive for all values of 1 from -5 and for the values greater than 1. Hence the solutions are x≥+1 and x≤−5x\ge +1\text{ and }x\le -5.
So, the solution is x(−∞,−5]∪[1,∞)x\left( -\infty ,-5 \right]\cup \left[ 1,\infty \right).

Note: We can answer in the form of inequalities as x>1x>1 or x<5x<5 or x≥2x\ge 2 or we can change it into the interval form. Remember that [ is used when the last value is included in the solution. If we have inequalities as x>2x>2, then our solution ends with ) in the interval form. If we have inequalities as x≥ax\ge a our solution ends up by ] in the interval form. We need to be careful while solving the problems.