Question

How do you solve ${{x}^{2}}=13x-42$?

Answer 1

In this problem we have given an equation and asked to find the solution. We can observe that the given equation is a quadratic equation. We can observe that the given equation is not in the standard form, so we will convert it into the standard form which is $a{{x}^{2}}+bx+c$. Now we will compare the obtained equation with the standard equation $a{{x}^{2}}+bx+c$ and, now we will calculate the value of $ac$ and write the factors of the value $ac$. From the factors of the $ac$, we will consider any two factors such that $b={{x}_{1}}+{{x}_{2}}$, $ac={{x}_{1}}\times {{x}_{2}}$. Now we will split the middle term $bx$ by using the value $b={{x}_{1}}+{{x}_{2}}$. Now we will take appropriate terms as common and simplify the equation to get the factors of the quadratic equation. After calculating the factors, we will equate each factor to zero and simplify them to get the roots.

Complete step by step solution:
Given equation, ${{x}^{2}}=13x-42$.
Shifting the all the terms we have in the RHS to LHS and changing their signs, then we will get
$\Rightarrow {{x}^{2}}-13x+42=0$
We have the quadratic equation ${{x}^{2}}-13x+42$ in the above equation. Considering this quadratic equation and comparing it with the standard form of the quadratic equation $a{{x}^{2}}+bx+c$, then we will get
$a=1$, $b=-13$, $c=42$.
Now the value of $ac$ will be
$\begin{aligned} & \Rightarrow ac=1\times 42 \\\ & \Rightarrow ac=42 \\\ \end{aligned}$
Factors of the value $42$ are $1$, $2$, $3$, $6$, $7$, $14$, $21$, $42$. From the above factors we can write that
$\begin{aligned} & -6\times -7=42 \\\ & -6-7=-13 \\\ \end{aligned}$
So, we can split the middle term which is $-13x$ as $-6x-7x$. Now the quadratic equation is modified as
$\Rightarrow {{x}^{2}}-13x+42={{x}^{2}}-6x-7x+42$
Taking $x$ as common from the terms ${{x}^{2}}-6x$ and taking $-7$ as common from the terms $-7x+42$, then we will get
$\Rightarrow {{x}^{2}}-13x+42=x\left( x-6 \right)-7\left( x-6 \right)$
Now taking $x-6$ as common from the above equation, then we will get
$\Rightarrow {{x}^{2}}-13x+42=\left( x-6 \right)\left( x-7 \right)$
Equating each factor to zero, then we will get
$\begin{aligned} & x-6=0\text{ or }x-7=0 \\\ & \Rightarrow x=6\text{ or }x=7 \\\ \end{aligned}$
Hence the roots of the given equation ${{x}^{2}}=13x-42$ are $x=6,7$

Note: We can also observe the roots of the given equation when we plot a diagram for the given equation. The graph of the given equation will be

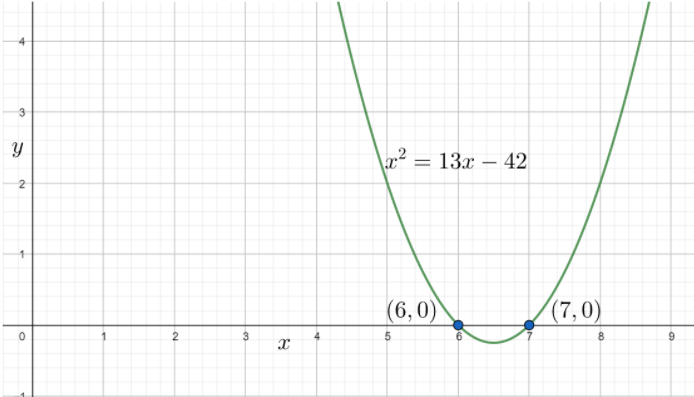
From the above graph we can also see that the roots of the given equation are $x=6,7$.