Question

How do you solve ${{x}^{2}}+12x+20=0$ by completing the square?

Answer 1

In the problem they have mentioned to use the method of completing the square. We know that the method of completing the square is used to solve or find the roots of a quadratic equation. So first we will check whether the given equation is a quadratic equation or not. If the given equation is a quadratic equation and which is in the form of $a{{x}^{2}}+bx+c=0$, then we will go to the further steps. In the first step we will divide the given equation with the coefficient of ${{x}^{2}}$ to get the coefficient of ${{x}^{2}}$ as $1$. In the step two we will add and subtract the square of the half of the coefficient of $x$ in the above equation and rearrange the obtained equation, then we will apply the formula either ${{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$ or ${{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}$ based the obtained equation in step two. In step three we will simplify and move the constants to another side of the equation. In step four we will apply square roots on both sides of the equation and simplify it to get the value of $x$.

Complete step by step solution:
Given equation, ${{x}^{2}}+12x+20=0$
We can clearly see that the above equation is a quadratic equation, so we can use the method of completing the square to solve the given equation.
Comparing the given equation with $a{{x}^{2}}+bx+c=0$, then we will get
$a=1$, $b=12$, $c=20$.
We have the value $a=1$, so we are not dividing the given equation with a coefficient of ${{x}^{2}}$.
In the above equation the coefficient of $x$ is $12$. Adding the square of half of the coefficient of $x$ in the above equation, then we will get
$\begin{aligned} & \Rightarrow {{x}^{2}}+12x+20+{{\left( \dfrac{12}{2} \right)}^{2}}-{{\left( \dfrac{12}{2} \right)}^{2}}=0 \\\ & \Rightarrow {{x}^{2}}+12x+20+{{\left( 6 \right)}^{2}}-{{\left( 6 \right)}^{2}}=0 \\\ \end{aligned}$
Rearranging and rewriting the terms in the above equation, then we will get
$\Rightarrow {{x}^{2}}+2\left( 6 \right)\left( x \right)+{{\left( 6 \right)}^{2}}+20-36=0$
We know that ${{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$, then we will get
$\Rightarrow {{\left( x+6 \right)}^{2}}-16=0$
Taking the constants in the above equation to the other side of the equation, then we will get
$\Rightarrow {{\left( x+6 \right)}^{2}}=16$
Applying square root on both side of the above equation, then we will get
$\begin{aligned} & \Rightarrow \sqrt{{{\left( x+6 \right)}^{2}}}=\sqrt{16} \\\ & \Rightarrow x+6=\pm 4 \\\ \end{aligned}$
From the above equation, we will get
$x+6=4$ or $x+6=-4$
Simplifying the above equations, then
$\begin{aligned} & x=4-6 \\\ & \Rightarrow x=-2 \\\ \end{aligned}$ or
$\begin{aligned} & x=-4-6 \\\ & \Rightarrow x=-10 \\\ \end{aligned}$
Hence the roots of the given equation ${{x}^{2}}+12x+20=0$ are $x=-2,-10$.

Note: We can also plot the graph of the given equation to get the roots of the given equation. When we plot the graph of the equation ${{x}^{2}}+12x+20=0$, then we will get

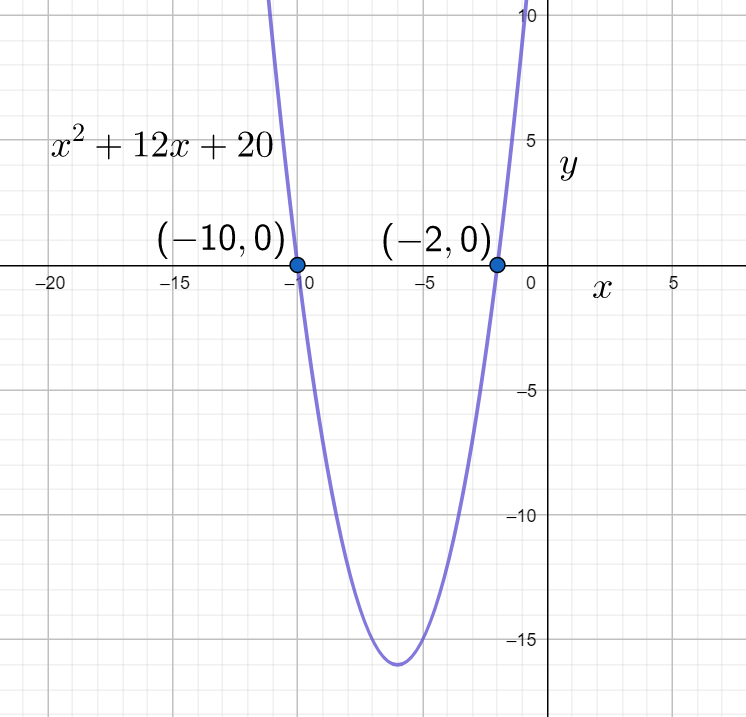
From the above graph also, we can write the roots of the given equation ${{x}^{2}}+12x+20=0$ are $x=-2,-10$.