Solveeit Logo
Login

Question

Question: How do you solve the triangle if it has legs with lengths of \( 18 \) and \( 28 \) and there is a \(...

How do you solve the triangle if it has legs with lengths of 1818 and 2828 and there is a 9090 degree angle, X and Y are the other two angles ?

Explanation

Solution

Hint : The given question requires to solve the right angled triangle given the length of the two legs as 1818 units and 2828 units. Solving a triangle means that we have to find all the missing sides and angles of the given triangle. So, we have to find the length of the hypotenuse of the given right angled triangle and the measure of the other two angles. This can be done easily using the Pythagoras theorem and trigonometry.

Complete step by step solution:
Let us consider a right angled triangle XYZ with Z=90∘Z = {90^ \circ } . Also,
Considering the given right angle is right angled at Z, that is ∠Z=90∘\angle Z = {90^\circ } . So, the figure is given below:

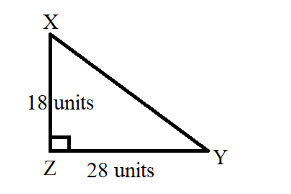
Now, length of XZ =18= 18 units
Also, length of YZ =28= 28 units
Following the Pythagoras theorem, we have (Hypotenuse)2=(Base)2+(Altitude)2{\left( {Hypotenuse} \right)^2} = {\left( {Base} \right)^2} + {\left( {Altitude} \right)^2}.
So, applying the Pythagoras theorem in the given triangle ABC, we get, (XY)2=(XZ)2+(YZ)2{\left( {XY} \right)^2} = {\left( {XZ} \right)^2} + {\left( {YZ} \right)^2} .
So, (XY)2=(18)2+(28)2{\left( {XY} \right)^2} = {\left( {18} \right)^2} + {\left( {28} \right)^2}
⇒(XY)2=324+784\Rightarrow {\left( {XY} \right)^2} = 324 + 784
⇒(XY)2=1108\Rightarrow {\left( {XY} \right)^2} = 1108
⇒XY=1108\Rightarrow XY = \sqrt {1108}
⇒XY=33.286\Rightarrow XY = 33.286 units (approximately)
Now, we know all the sides of the triangle.
We can also find the remaining two angles with the help of trigonometry.
We know that, tan⁡Y=1828=(914)\tan Y = \dfrac{{18}}{{28}} = \left( {\dfrac{9}{{14}}} \right) .
⇒Y=tan⁡−1(914)\Rightarrow Y = {\tan ^{ - 1}}\left( {\dfrac{9}{{14}}} \right)
Similarly for the angle X, we have, tan⁡X=2818=(149)\tan X = \dfrac{{28}}{{18}} = \left( {\dfrac{{14}}{9}} \right) .
⇒X=tan⁡−1(149)\Rightarrow X = {\tan ^{ - 1}}\left( {\dfrac{{14}}{9}} \right)
So, this is the solution of the triangle given to us.

Note : For solving such type of question, where we need to find the third side of a triangle using the Pythagoras theorem, we need to know the position of right angle in the triangle beforehand since we need to know which of the three sides is the hypotenuse of the right angled triangle and then apply the Pythagoras theorem (Hypotenuse)2=(Base)2+(Altitude)2{\left( {Hypotenuse} \right)^2} = {\left( {Base} \right)^2} + {\left( {Altitude} \right)^2}.