Question

How do you solve the system $x+2y=13$ and $3x-5y=6$ using substitution?

Answer 1

In the given question we are given two linear equations which we need to solve for two unknown variables x and y using the method of substitution and hence obtain the value of x and y. For this we first find the relation of one variable with respect to another variable and then put that relation in another equation and then solve that.

Complete step-by-step solution:
According to the given question, we have two linear equations with us such that we need to solve them for x and y unknowns.
Also, we are given that we need to use the method of substitution. Now, for that what we need to do is we need to attain the relation between the two variables from one of the two equations and then substitute that relation in another equation and then attain the value of one variable and after substituting that value in relation we will attain the value of another variable also.
The graph for the given two equations is as follows:

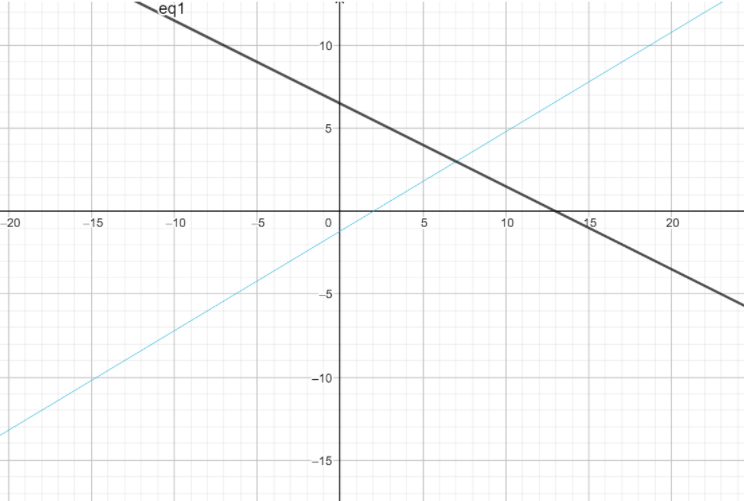
Now, mathematically we can see that
$\begin{aligned} & 3x-5y=6 \\\ & \Rightarrow 3x=6+5y \\\ & \Rightarrow x=2+\dfrac{5}{3}y \\\ \end{aligned}$
So, here we got the relation between x and y from the second equation. Now substituting this relation in place of x in the first equation we get, $2+\dfrac{5}{3}y+2y=13$ .
Now we can solve this for y and we will get
$\begin{aligned} & 2+\dfrac{5}{3}y+2y=13 \\\ & \Rightarrow \dfrac{11}{3}y=11 \\\ & \Rightarrow y=3 \\\ \end{aligned}$
Therefore $y=3$ and now substituting this in the relation we get $x=7$ .
Hence, after solving the given two equations using substitution, we get $x=7$and $y=3$.

Note: In the given question we must remember that from which equation we have taken the relation and which equation we will need to get the values of the unknowns. Also, try to remove the fractional coefficient if present in order to reduce the complexity.