Question

How do you solve the system of equations ${{x}^{2}}+{{y}^{2}}\ge 4$ and $4{{x}^{2}}+9{{y}^{2}}\le 36$ by graphing?

Answer 1

To solve the system of equations, we are going to draw each of these equations on the graph paper and then the common region which will come from the intersection of these two equations on the graph. The first equation which is given as ${{x}^{2}}+{{y}^{2}}\ge 4$ is the equation of a circle and the other equation which is given as $4{{x}^{2}}+9{{y}^{2}}\le 36$ is the equation of an ellipse so solve the equations and find the value of radius of the circle and the major and minor axis of the ellipse.

Complete step-by-step solution:
In the above problem, we have given two equations as follows:
${{x}^{2}}+{{y}^{2}}\ge 4$;
$4{{x}^{2}}+9{{y}^{2}}\le 36$
Now, let us scrutinize each of the equations one by one. Analyzing the first equation we get,
$\Rightarrow {{x}^{2}}+{{y}^{2}}\ge 4$
Let us remove the greater than sign from the above inequality and then analyze it.
$\Rightarrow {{x}^{2}}+{{y}^{2}}=4$
We know that equation of the circle is of the form ${{x}^{2}}+{{y}^{2}}={{r}^{2}}$ and the above equation is also in this form so rewriting the above equation we get,
$\Rightarrow {{x}^{2}}+{{y}^{2}}={{2}^{2}}$
From the above equation, 2 is the radius of the circle so now, let us bring the greater than sign again in the above inequality to graph the above equation.
$\Rightarrow {{x}^{2}}+{{y}^{2}}\ge {{2}^{2}}$
Now, to graph the above equation, we are going to draw the circle with centre (0, 0) and radius as 2 on the graph and we get,

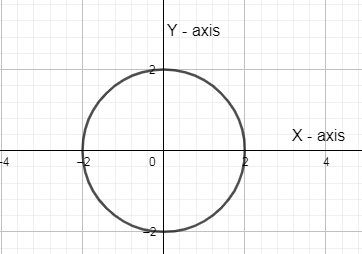
In the above circle, you can see that radius is 2 and centre is (0, 0). Now, the region which will be possible according to the equation given above is the area which lies outside of the circle and also contains the boundary of the circle.
Now, we are going to draw the second equation in the same graph in which we have drawn the circle.
The second equation given in the above problem is as follows:
$4{{x}^{2}}+9{{y}^{2}}\le 36$
Let us remove the inequality sign first then the above equation will look like:
$\Rightarrow 4{{x}^{2}}+9{{y}^{2}}=36$
Dividing 36 on both the sides of the above equation and we get,
$\Rightarrow \dfrac{4{{x}^{2}}}{36}+\dfrac{9{{y}^{2}}}{36}=1$
Solving the above equation by dividing 36 written in the denominator by 4 in the coefficient of ${{x}^{2}}$ and dividing 36 by 9 in the coefficient of ${{y}^{2}}$ we get,
$\Rightarrow \dfrac{{{x}^{2}}}{9}+\dfrac{{{y}^{2}}}{4}=1$
Now, the above equation will look like the equation of an ellipse and we know that equation of ellipse is of the form:
$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$
So, the second equation is an equation of an ellipse and rewriting the second equation in the form of an ellipse equation we get,
$\Rightarrow \dfrac{{{x}^{2}}}{{{3}^{2}}}+\dfrac{{{y}^{2}}}{{{2}^{2}}}=1$
From the above equation, major axis of the above equation is 3 and minor axis of the above equation is 2 so graphing this equation of ellipse we get,

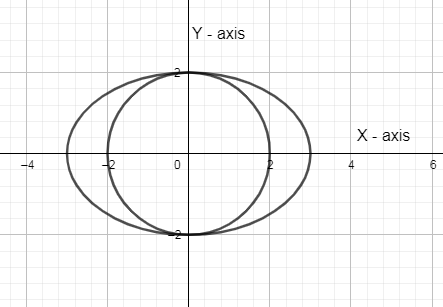
Now, we are going to put the inequality in the second equation and we get,
$\Rightarrow \dfrac{{{x}^{2}}}{{{3}^{2}}}+\dfrac{{{y}^{2}}}{{{2}^{2}}}\le 1$
The region which is suggested by the above equation lies inside the ellipse and includes the circumference of the ellipse. Hence, the common region is shown as:

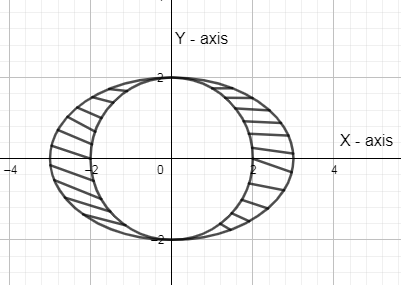
In the above figure, the shaded region is the solution of the system of equations.

Note: The mistake that could be possible is that you might not include the circumference of circle and ellipse so make sure you will include the circumferences of circle and ellipse. And the reason for including the circumference of circle and ellipse is that in the inequalities given above we have given the equality sign also which is saying that we have to take into account all the points lying on the circle and ellipse.
These are the inequalities given below:
${{x}^{2}}+{{y}^{2}}\ge 4$;
$4{{x}^{2}}+9{{y}^{2}}\le 36$
As you can see the equality sign here so this is the equality sign we are talking about.