Question

How do you solve the system by graphing $x + 2y = 4$ and $2x + 4y = 8$?

Answer 1

In this question we need to find the solution of a system of linear equation by graphing method and equation of systems are $x + 2y = 4$ and $2x + 4y = 8$. We will plot both equations of lines on the graph. We need to know the condition of types of solution of system linear equations. A system of linear can have finite, infinite or no solutions.

Complete step by step solution:
Let us try to solve this question in which we are asked to find the solution of the system of a linear equation by graphing method. To find the solution of the system of linear equations we will plot both equation $x + 2y = 4$ and $2x + 4y = 8$ on the graph. To plot these lines we need some points on both lines. We will first convert both lines into their slope intercept form and then find some point by assuming values of $x$.
Hence both equations of lines in slope intercept form $y = mx + c$, where $m$ slope and $c$ is the intercept of line. Here is the slope-intercept form of both equations.
Line $x + 2y = 4$
$x + 2y = 4 \\\ 2y = - x + 4 \\\ y = \dfrac{{ - x}}{2} + 2 \\\$
Hence the slope is $m = \dfrac{{ - 1}}{2}$ and intercept $c = 2$for line$x + 2y = 4$.
Here are the some point which line on the line $x + 2y = 4$, are $( - 2,3),\left( { - 1,\dfrac{5}{2}} \right),(0,2),\left( {1,\dfrac{3}{2}} \right)and(2,1)$which we found by assuming values of $x$.
Line $2x + 4y = 8$
$2x + 4y = 8 \\\ 4y = - 2x + 8 \\\ y = \dfrac{{ - 2x}}{4} + \dfrac{8}{4} \\\ y = \dfrac{{ - x}}{2} + 2 \\\$
Hence the slope is $m = \dfrac{{ - 1}}{2}$ and intercept $c = 2$ for line $2x + 4y = 8$.
Here are the some point which line on the line $x + 2y = 4$, are $( - 2,3),\left( { - 1,\dfrac{5}{2}} \right),(0,2),\left( {1,\dfrac{3}{2}} \right) and (2,1)$ which we found by assuming values of $x$.
Since both lines have a set of points which are common and our given system of linear equations has infinitely many solutions. When we plot the graph of an equation we have only one line on the graph we have a case of overlapping lines. We can also see that both lines are constant multiples of each other. Here is the graph of a given system of linear equations.

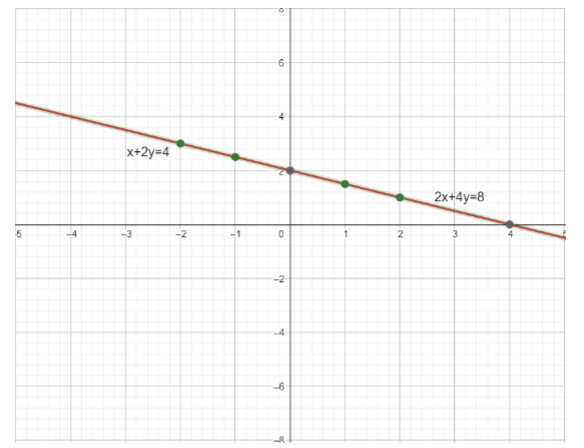
From the graph we can see that the line in green is $x + 2y = 4$ and $2x + 4y = 8$ is in red color. Both are overlapping each other. Hence the above system of linear equations has infinitely many solutions.

Note: We can also solve systems of linear equations by elimination method but here we specified to solve using graphing methods. You can try on your own to solve for a given system of linear equations to check if you are getting the same solution or not.