Question

How do you solve the system by graphing the linear system $2x-y=5$ and $3x+2y=4$ ?

Answer 1

The above 2 equations are of straight lines. The solution to the system of equations will be the intersection between 2 lines. There will be no solution if 2 lines are parallel to each other and infinite solution if both lines are the same.

Complete step-by-step answer:
General formula for the line is $y=mx+c$
$2x-y=5$ and $3x+2y=4$ are equations of straight lines. The intersection point will be the solution of the system.
General equation for the line is $y=mx+c$ where m is the slope and c is the y intercept, we can write $2x-y=5$ as $y=2x-5$ and if we compare $y=2x-5$ with $y=mx+c$ we get the slope is 2 and y intercept is equal to – 5, in $3x+2y=4$ the slope is $-\dfrac{3}{2}$ and y intercept is equal to 2 so let’s draw the graph and find out the point of intersection.

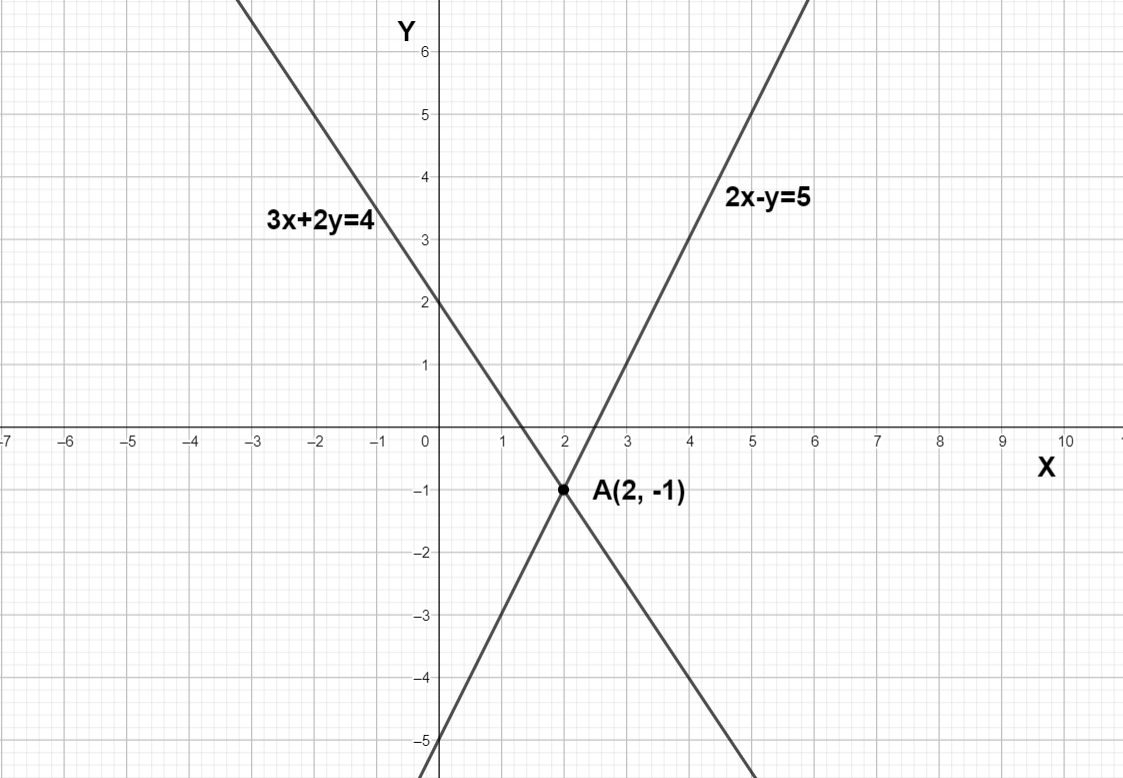
We can see that the point of intersection is A(2 , - 1) x coordinate is the solution. So 2 is the solution.

Note: Another method is to solve by determinant method
Suppose there are 2 linear equation ${{a}_{1}}x+{{b}_{1}}y={{c}_{1}}$ and ${{a}_{2}}x+{{b}_{2}}y={{c}_{2}}$ the solution to this problem let’s take
D= $\left| \begin{matrix} {{a}_{1}} & {{b}_{1}} \\\ {{a}_{2}} & {{b}_{2}} \\\ \end{matrix} \right|$
A= $\left| \begin{matrix} {{b}_{1}} & {{c}_{1}} \\\ {{b}_{2}} & {{c}_{2}} \\\ \end{matrix} \right|$
B= $\left| \begin{matrix} {{a}_{1}} & {{c}_{1}} \\\ {{a}_{2}} & {{c}_{2}} \\\ \end{matrix} \right|$
$x=-\dfrac{A}{D}$ and $y=\dfrac{B}{D}$ Where $D\ne 0$
If $D=0$ and any one of A and B is not equal to 0 then there will be no solution for the system of equation
If $D=A=B=0$ there will be infinitely many solutions to the system of equations.
If $D\ne 0$ there will be one solution for the system of equations.
In this case ${{a}_{1}}=2,{{b}_{1}}=-1,{{c}_{1}}=5$ and ${{a}_{2}}=3,{{b}_{2}}=2,{{c}_{2}}=4$
Solving the determinant D = 7 , A= - 14 and B = -7
So $x=-\dfrac{A}{D}$
So x = 2

And $y=\dfrac{B}{D}$= - 1
While solving the system of linear equations we can imagine the equation having 2 unknown as equations of straight in 2-D Cartesian plane so 2 equations means 2 lines will intersect at 1 point unless both lines are parallel or both lines are overlapping. Same goes with 3 unknowns: we can imagine the equations as equations of plane in 3D geometry and then solve for the unknown variables.