Question

How do you solve the series $\sin \left( \dfrac{1}{n} \right)$ using a comparison test?

Answer 1

We know that there is a property of $\sin x$ that at very small values of $x$, meaning when x is attaining to 0 then $\sin x$ is equal to $x$ so we can compare the behavior of $\sin x$ with $x$. And in the given expression $\sin \left( \dfrac{1}{n} \right)$ we can compare its behavior with $\dfrac{1}{n}$.

Complete step by step answer:
In the above problem, we are asked to solve the following trigonometric expression using comparison test:
$\sin \left( \dfrac{1}{n} \right)$
We know that there is a property of $\sin x$ that at very small angles like the value of angles tending to 0, $\sin x=x$ so in order to understand the behavior of $\sin x$ we can study the behavior of x.
Now, at very small angles:
$\sin \left( \dfrac{1}{n} \right)=\dfrac{1}{n}$
When n is very large like when n is tending to infinity then $\dfrac{1}{n}$ will tend to 0 (or a very small value) so at that point we can compare $\sin \left( \dfrac{1}{n} \right)$ with $\dfrac{1}{n}$.
Now, according to convergence and divergence theory we know that the expression $\dfrac{1}{n}$ will diverge at infinity so the expression $\sin \left( \dfrac{1}{n} \right)$ will also diverge at infinity.

Note:
In the below diagram, we are showing the property that at very small angles $\sin x$ and $x$ are having the same behavior.

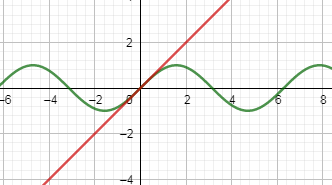
In the above figure, the curvy diagram is of $\sin x$ and the straight line is of the function x. And when you zoom into very small values of x then both $\sin x\And x$ will show the same nature.
Now, zooming in to very small values of “x” section we get,

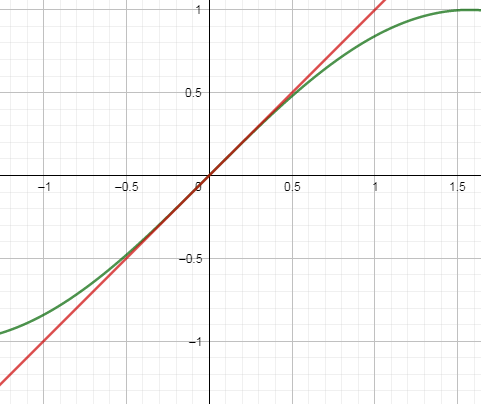
As you can clearly see from the above figure that $\sin x\And x$ are overlapping on each other in the very small values of “x” portion.