Question

How do you solve the inequality ${x^2} - 10 < 3x$?

Answer 1

We have to find all possible values of $x$ satisfying given inequality. For this first, subtract $3x$ from both sides of the equation. Then, factor the polynomial using the middle term splitting method. Next, obtain the system of linear inequations. Then, solve each inequation and obtain their solution sets. Also, represent them on a real line. Then, find the intersection of the solutions sets obtained by taking the help of the graphical representation of the solution sets. Thus, the set obtained is the required solution set of the given system of inequations.
Formula used:
In the process of solving an inequation, we use mathematical simplifications which are governed by the following rules:
Rule 1 Same number may be added to (or subtracted from) both sides of an inequation without changing the sign of inequality.
Rule 2 Both sides of an inequation can be multiplied (or divided) by the same positive real number without changing the sign of inequality. However, the sign of inequality is reversed when both sides of an inequation are multiplied or divided by a negative number.
Rule 3 Any term of an inequation may be taken to the other side with its sign changed without affecting the sign of inequality.

Complete step-by-step solution:
Given: ${x^2} - 10 < 3x$
We have to find all possible values of $x$ satisfying given inequality.
First, subtract $3x$ from both sides of the equation.
${x^2} - 3x - 10 < 0$
Now, we have to factor ${x^2} - 3x - 10$.
For factorising an algebraic expression of the type $a{x^2} + bx + c$, we find two factors $p$ and $q$ such that
$ac = pq$ and $p + q = b$
Here, $a = 1,b = - 3,c = - 10$
So, $ac = - 10$.
We can take $p = 2,q = - 5$ as $2 \times \left( { - 5} \right) = - 10 = ac$ and $2 + \left( { - 5} \right) = - 3 = b$.
So, we get ${x^2} + 2x - 5x - 10 < 0$.
Take common terms.
$\Rightarrow x\left( {x + 2} \right) - 5\left( {x + 2} \right) < 0$
$\Rightarrow \left( {x + 2} \right)\left( {x - 5} \right) < 0$
Since, the product of two factors is negative.
So, one factor will be less than 0 and other will be greater than 0.
Thus, $x + 2 < 0,x - 5 > 0$ or $x + 2 > 0,x - 5 < 0$.
The system of inequalities is
$x + 2 < 0$…(i)
$x - 5 > 0$…(ii)
So, first we will solve inequation (i).
Collect all terms involving the variable on one side of the inequation and the constant terms on the other side and simplify both sides of inequality in their simplest forms to reduce the inequation in the form $ax < b$.
For this, subtract $2$ to both sides of inequation (i).
So, by rule 1, $x < \- 2$
Hence, any real number less than $- 2$ is a solution of inequation (i).
These solutions can be graphed on real line as shown below:

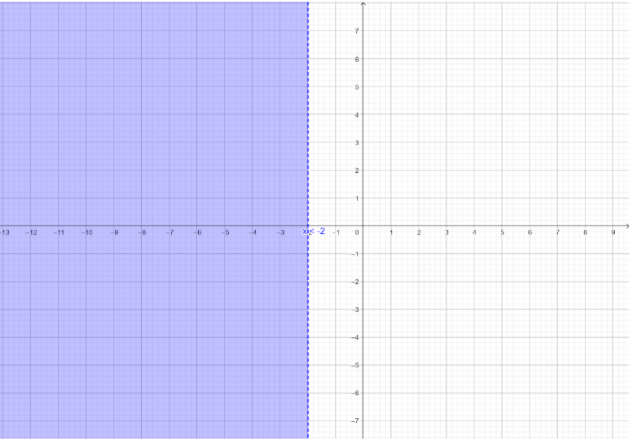
The solution set of inequation (i) is $\left( { - \infty , - 2} \right)$.
Now, we will solve inequation (ii).
Collect all terms involving the variable on one side of the inequation and the constant terms on the other side and simplify both sides of inequality in their simplest forms to reduce the inequation in the form $ax > b$.
For this, add $5$ to both sides of inequation (ii).
So, by rule 1, $x > 5$
Hence, any real number greater than $5$ is a solution of inequation (ii).
These solutions can be graphed on real line as shown below:

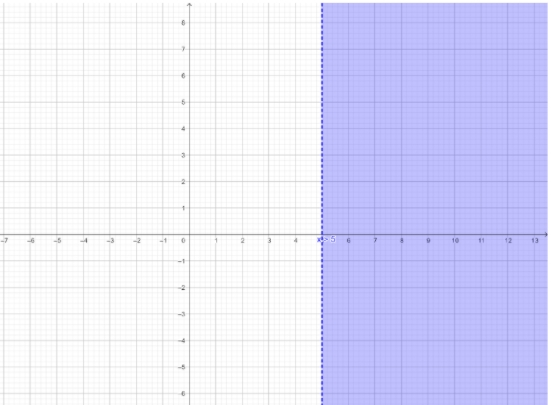
The solution set of inequation (ii) is $\left( {5,\infty } \right)$.
We observe that there is no common solution of the two inequalities.
The system of inequalities are
$x + 2 > 0$…(iii)
$x - 5 < 0$…(iv)
So, first we will solve inequation (iii).
Collect all terms involving the variable on one side of the inequation and the constant terms on the other side and simplify both sides of inequality in their simplest forms to reduce the inequation in the form $ax > b$.
For this, subtract $2$ to both sides of inequation (iii).
So, by rule 1, $x > - 2$
Hence, any real number greater than $- 2$ is a solution of inequation (iii).
These solutions can be graphed on real line as shown below:

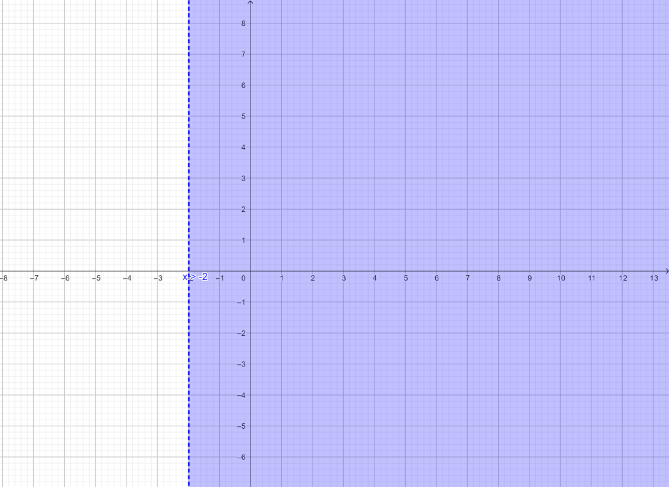
The solution set of inequation (iii) is $\left( { - 2, + \infty } \right)$.
Now, we will solve inequation (iv).
Collect all terms involving the variable on one side of the inequation and the constant terms on the other side and simplify both sides of inequality in their simplest forms to reduce the inequation in the form $ax < b$.
For this, add $5$ to both sides of inequation (iv).
So, by rule 1, $x < 5$
Hence, any real number less than $5$ is a solution of inequation (iv).
These solutions can be graphed on real line as shown below:

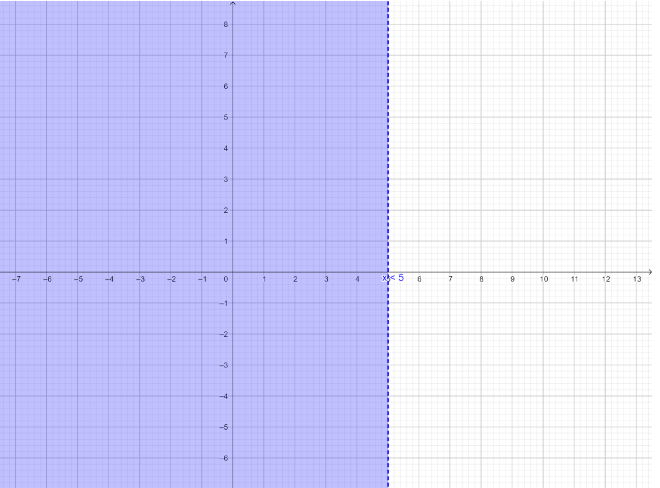
The solution set of inequation (iv) is $\left( { - \infty ,5} \right)$.
We observe that $\left( { - 2,5} \right)$ is a common solution of the two inequalities.
Thus, $\left( { - 2,5} \right)$ is the required solution set of the given equation.

Note: In order to solve a system of linear inequalities in one variable, we follow the following algorithm.
Algorithm:
Step I Obtain the system of linear inequations.
Step II Solve each inequation and obtain their solution sets. Also, represent them on a real line.
Step III Find the intersection of the solution sets obtained in step II by taking the help of the graphical representation of the solution sets in step II.
Step IV The set obtained in step III is the required solution set of the given system of inequations.