Question

How do you solve the inequality$\dfrac{1}{{x + 1}} \succ \dfrac{3}{{x - 2}}?$

Answer 1

The given question describes the operation of addition/ subtraction/ multiplication/ division. In this question, we have to find the value of$x$. At first, we would arrange the fraction terms to one side. After that, we have to find the final condition to find the value $x$. In this question, we have to use a number line to assume the value of$x$ and compare it with the final condition.

Complete step by step solution:
In this question, we have to solve the following inequality terms,
$\dfrac{1}{{x + 1}} \succ \dfrac{3}{{x - 2}}$

First, we have to arrange the fraction terms into one side of the equation. So, the above
equation can also be written as,

$$\dfrac{3}{{x - 2}} \prec \dfrac{1}{{x + 1}} \\\ \dfrac{3}{{x - 2}} - \dfrac{1}{{x + 1}} \prec 0 \\\$$

Using cross-multiplication, we get

$$\dfrac{{\left( {3\left( {x + 1} \right)} \right) - \left( {1\left( {x - 2} \right)} \right)}}{{\left( {x - 2} \right)\left( {x + 1} \right)}} \prec 0 \\\ \dfrac{{3x + 3 - x + 2}}{{\left( {x - 2} \right)\left( {x + 1} \right)}} \prec 0 \\\$$

Let’s solve the numerator using arithmetic operations,

$$\dfrac{{3x + 3 - x + 2}}{{\left( {x - 2} \right)\left( {x + 1} \right)}} \prec 0 \\\ \dfrac{{2x + 5}}{{\left( {x - 2} \right)\left( {x + 1} \right)}} \prec 0 \\\$$

So, the final condition is,
\dfrac{{2x + 5}}{{\left( {x - 2} \right)\left( {x + 1} \right)}} \prec 0$$$$ \to \left( 1 \right)

For finding the value of$x$ we have to assume,
(Case: 1) $2x + 5 = 0$
(Case: 2) $x - 2 = 0$
(Case: 3) $x + 1 = 0$

In case: 1 we get,

$$2x + 5 = 0 \\\ 2x = - 5 \\\ x = \dfrac{{ - 5}}{2} \\\$$

In case: 2 we get,

$$x - 2 = 0 \\\ x = 2 \\\$$

In vase: 3 we get,

$$x + 1 = 0 \\\ x = - 1 \\\$$

So finally we have,
$x = \dfrac{{ - 5}}{2},x = 2$and$x = - 1$

Let’s mark the above-mentioned values in the number line,

We have three options for$x$value. Now we need to find the correct$x$value among the three answers. Here we have intervals $\left( { - \infty ,\dfrac{{ - 5}}{2}} \right),\left( {\dfrac{{ - 5}}{2}, - 1} \right),\left( { - 1,2} \right)and\left( {2,\infty } \right)$

To find the correct interval we have to assume anyone value with each interval and substitute that value in the equation$\left( 1 \right)$

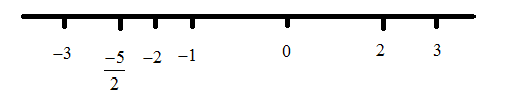
In the interval $\left( { - \infty ,\dfrac{{ - 5}}{2}} \right)$ we assume$- 3$. So, the final
condition$\left( 1 \right)$becomes,

$\left( 1 \right) \to \dfrac{{2x + 5}}{{\left( {x - 2} \right)\left( {x + 1} \right)}} \prec 0$

Where, $x = - 3$

$\dfrac{{2\left( { - 3} \right) + 5}}{{\left( { - 3 - 2} \right)\left( { - 3 + 1} \right)}} \prec 0$

$\dfrac{{ - 6 + 5}}{{\left( { - 5} \right)\left( { - 2} \right)}} \prec 0$

$\dfrac{{ - 1}}{{10}} \prec 0$

The above equation satisfies the condition.

In the interval$\left( {\dfrac{{ - 5}}{2}, - 1} \right)$, we assume $x = - 2$

$\left( 1 \right) \to \dfrac{{2x + 5}}{{\left( {x - 2} \right)\left( {x + 1} \right)}} \prec 0$

$\dfrac{{2\left( { - 2} \right) + 5}}{{\left( { - 2 - 2} \right)\left( { - 2 + 1} \right)}} \prec 0$

$\dfrac{{ - 4 + 5}}{{ - 1 \times - 4}} \prec 0$

$\dfrac{1}{4} \prec 0$

The above equation doesn’t satisfy the condition.

In the interval$\left( { - 1,2} \right)$, we assume$x = 0$

$\left( 1 \right) \to \dfrac{{2x + 5}}{{\left( {x - 2} \right)\left( {x + 1} \right)}} \prec 0$

$\dfrac{{2\left( 0 \right) + 5}}{{\left( {0 - 2} \right)\left( {0 + 1} \right)}} \prec 0$

$\dfrac{{ - 5}}{2} \prec 0$

The above equation satisfies the condition.
In the interval$\left( {2,\infty } \right)$, we assume$x = 3$

$\left( 1 \right) \to \dfrac{{2x + 5}}{{\left( {x - 2} \right)\left( {x + 1} \right)}} \prec 0$

$\dfrac{{2\left( 3 \right) + 5}}{{\left( {3 - 2} \right)\left( {3 + 1} \right)}} \prec 0$

$\dfrac{{6 + 5}}{{4 \times 1}} \prec 0$

$\dfrac{{11}}{4} \prec 0$

The above equation doesn’t satisfy the condition.

So, the final answer is$x \in \left( { - \infty ,\left( {\dfrac{{ - 5}}{2}} \right)} \right) \cup \left( { - 1,2} \right)$

Note: The total limit of the number line is$\left( { - \infty , + \infty } \right)$. In this type of question we should use the arithmetic operation of addition/ subtraction/ multiplication/ division/ cross multiplication. Take care when assuming the value of$x$in the number line. If the$x$value is a fraction number, convert it into a decimal number for easy calculation.