Question

How do you solve the given inequality $-\dfrac{x}{x-3}\ge 0$?

Answer 1

We start solving the problem by making the necessary calculations in the given inequality. We then recall the fact that the inequality $\dfrac{a}{b}\le 0$ is possible only if (i) $a\ge 0$ and $b < 0$, (ii) $a\le 0$ and $b > 0$. We then take each condition and then make the necessary calculations to get the intervals of x satisfying those conditions. We then draw these intervals on the real number line to get the required answer.

Complete step by step answer:
According to the problem, we are asked to solve the given inequality $-\dfrac{x}{x-3}\ge 0$.
We have given the inequality $-\dfrac{x}{x-3}\ge 0$.
$\Rightarrow \dfrac{x}{x-3}\le 0$ ---(1).
We can see that L.H.S (Left Hand Side) of the equation (1) resembles $\dfrac{a}{b}\le 0$. We know that this is possible only if
(i) $a\ge 0$ and $b < 0$.
(ii) $a\le 0$ and $b > 0$.
Now, let us apply the condition $a\ge 0$ and $b < 0$.
So, we have $x\ge 0$ and $x-3 < 0$.
$\Rightarrow x\ge 0$ and $x < 3$.
Let us draw both the obtained intervals on the real number line and find the common interval.

We can see that the common interval is $0\le x < 3$.
$\Rightarrow x\in \left[ 0,3 \right)$ ---(2).
Now, let us apply the condition $a\le 0$ and $b > 0$.
So, we have $x\le 0$ and $x-3 > 0$.
$\Rightarrow x\le 0$ and $x > 3$.
Let us draw both the obtained intervals on the real number line and find the common interval.

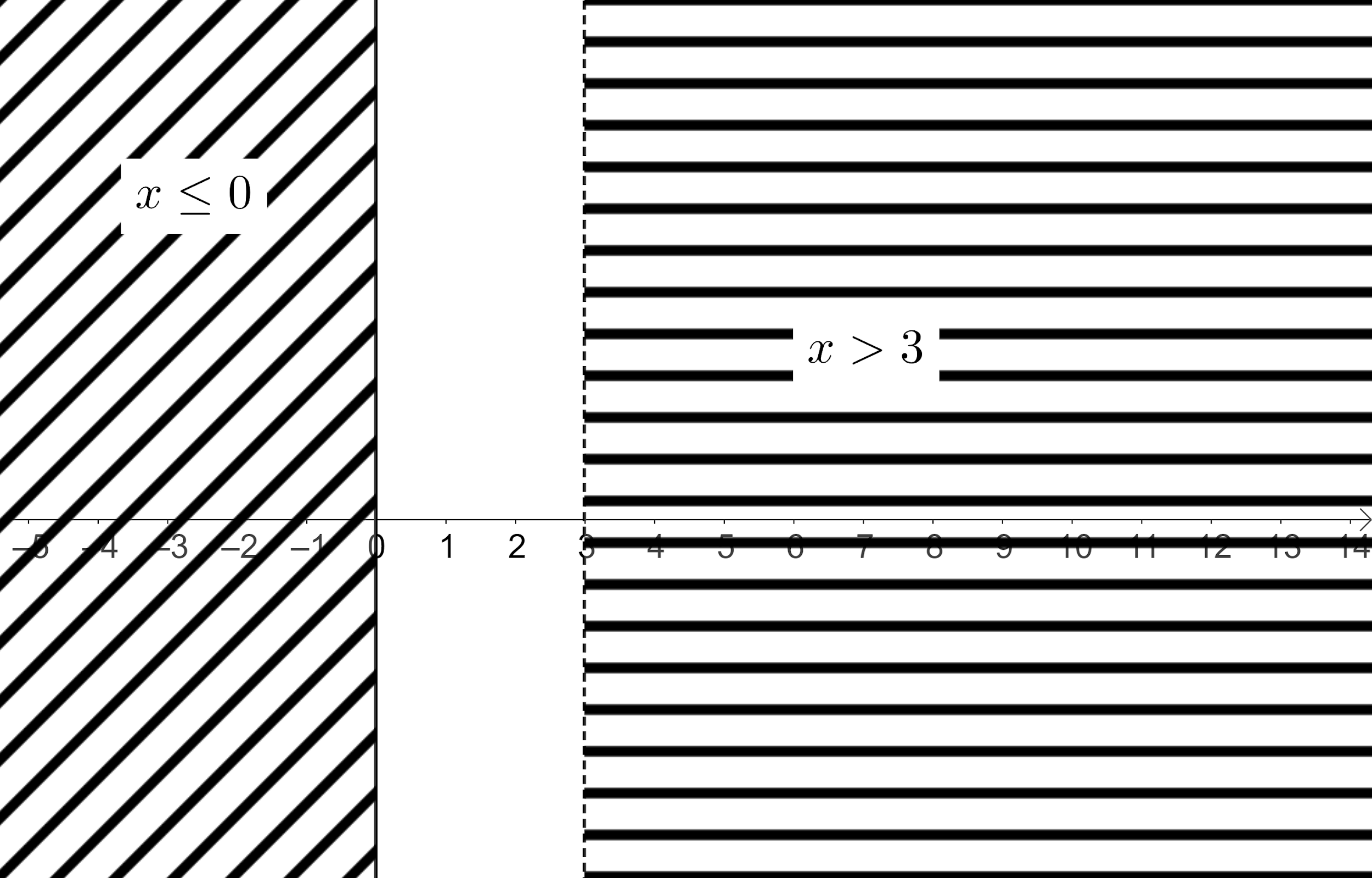
We can see that there is no common interval, which means that there is no solution for this condition.
From equation (2), we get that the solution set for the given inequality $-\dfrac{x}{x-3}\ge 0$ as $\left[ 0,3 \right)$.
$\therefore$ The solution set for the given inequality $-\dfrac{x}{x-3}\ge 0$ is $\left[ 0,3 \right)$.

Note:
We should not make calculation mistakes while solving this problem. We should keep in mind that “and” represents to take the values that both the inequalities are true unlike the “or”. We can also solve the given inequality by taking as $\dfrac{-x}{x-3}\ge 0$ and then applying the fact that that the inequality $\dfrac{a}{b}\ge 0$ is possible only if (i) $a\ge 0$ and $b > 0$, (ii) $a\le 0$ and $b < 0$. Similarly, we can expect problems to find the solution set for the inequality: $\dfrac{2-x}{x-3}\le 0$.