Question

How do you solve the equation $-{{x}^{2}}-7x=0$ by graphing?

Answer 1

In this question we have been with a polynomial equation which we have to solve by graphing. Graphing is a method by which the expression is expressed in the form of a two-dimensional graph and then the solutions are derived from it. We will use a graphing tool to first draw the graph of the equation and then solve for the values of the function at $0$ and get the required solutions.

Complete step by step solution:
We have the expression given to us as:
$\Rightarrow -{{x}^{2}}-7x=0$
Now since we have to find the solution of the function at the value $0$, we can write the expression in terms of a function of $x$ as:
$\Rightarrow f\left( x \right)=-{{x}^{2}}-7x$.
Now on using a graphing tool, we get the graph of the function as:

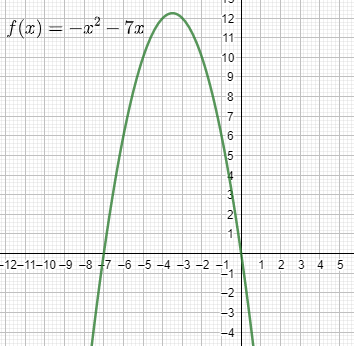
Now from the graph, we can see that the value of the function crosses $f\left( x \right)=0$ at two points which are $0$ and $-7$ therefore, on considering the points as $A$ and $B$, we get the graph as:

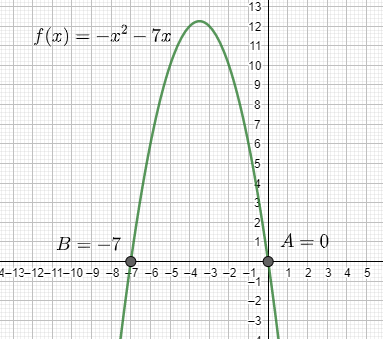
Therefore, through graphing $A=0$ and $B=-7$ are the two solutions to the expression.

Note: In this question we have used the method of graphing. This problem can also be solved by taking out the common values and equating them with $0$.
Consider the expression as:
$\Rightarrow -{{x}^{2}}-7x=0$
Now we can see that $x$ is common in both the terms therefore on taking it out as common, we get:
$\Rightarrow -x\left( x+7 \right)=0$
Now we know that when $ab=0$ either $a=0$ or $b=0$ therefore, we get:
$-x=0$ and $x+7=0$
On rearranging, we get:
$x=0$ and $x=-7$ as the two required solutions for the expression.