Question

How do you solve the AP calculus?

Answer 1

AP calculus is all about the concepts, methods, and applications of differential and integration. In the given question, we have been asked how to solve it. In order to answer the question, you need to first tell what concepts are included in this topic and how to solve that particular concept and the applications of each concept that is included in AP calculus.

Complete step by step solution:
AP calculus includes the concepts of:-
Limits and continuity
Differentiation
Derivative
Integration
Applications of integration

Limits and continuity:
A limit is the number that is approached by a function as an independent variable. For example: we have given the function $f\left( x \right)=2x$ where the limit of $f\left( x \right)\ as\ x=2$, it will be equal to $f\left( x \right)=2x=2\times 2=4$. Symbolically, it will be represented as $\underset{x\to 2}{\mathop{\lim f\left( x \right)}}\,=2\times 2=4$.

Continuity is another concept of AP calculus. A given function can either be continuous or it can be discontinuous. One of the easiest ways to find the continuity of any function is to trace the graph of a function by a pen, if there is need to lift up the pen then it will not be continuous and if you do not need to lift up the pen then we can say that the function is continuous.

For example: we have given the graph of a function,

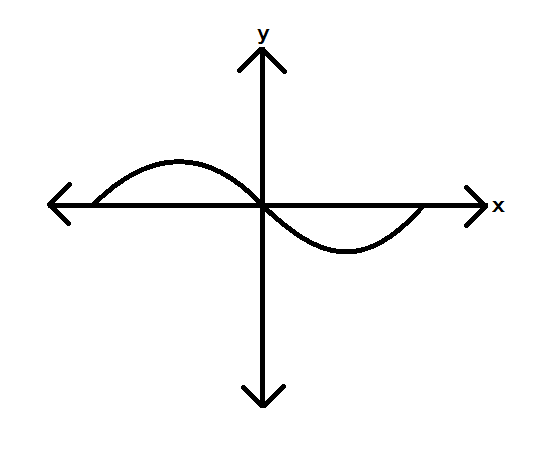
Suppose it is the given graph of the function. To find the continuity, we saw we not need to lift up the pen while tracing the graph of the function. Then we can say that the function is continuous.
Differentiation:
Differentiation tells us about the rate of change. It will allow us to find the rate of change of x with respect to y. there are various simple rules or formulas to differentiate the any equations, any polynomial, any function, any trigonometric functions etc.

If y is some function of x, then the derivative of y is written as $\dfrac{dy}{dx}$ or f’(x).

Some basic Differentiation formulas:

Sum or difference rule:
If $f\left( x \right)=u\left( x \right)\pm v\left( x \right)$
Then, $f'x=u'\left( x \right)\pm v'\left( x \right)$

Product rule:
If $f\left( x \right)=u\left( x \right)\times v\left( x \right)$
Then, $f'\left( x \right)=u'\left( x \right)\times v\left( x \right)+u\left( x \right)\times v'\left( x \right)$

Quotient rule:
If $f\left( x \right)=\dfrac{u\left( x \right)}{v\left( x \right)}$
Then, $f'\left( x \right)=\dfrac{u'\left( x \right)\times v\left( x \right)-u\left( x \right)\times v'\left( x \right)}{{{\left( v\left( x \right) \right)}^{2}}}$

Chain rule:
If a function y = f(x) = g(u) and if u = h(x), then chain rule for differentiation is,
$\dfrac{dy}{dx}=\dfrac{dy}{du}\times \dfrac{du}{dx}$
If f(x) = tan (x), then f’(x) = ${{\sec }^{2}}x$
If f(x) = cos(x), then f’(x) = $-{{\sin }^{2}}x$
If f(x) = sin(x), then f’(x) = cos(x)
If f(x) = ln(x), then f’(x) = $\dfrac{1}{x}$
If f(x) = ${{e}^{x}}$, then f’(x) = ${{e}^{x}}$
If f(x) = ${{x}^{n}}$, where n is any fraction or integer, then f’(x) = $n\times {{x}^{n-1}}$
If f(x) = k, where k is a constant then f’(x) = 0

Derivative:
Instantaneous rate of change of a quantity with respect to the other quantity. The derivative of a function is represented as,
$\mathop{\lim }_{x\to h}\dfrac{f\left( x+h \right)-f\left( x \right)}{h}=A$

Integration:
Integration is just opposite of differentiation. Differentiation refers to dividing a part into many small parts whereas integration refers to a collection of various small parts to make a whole. In integration there are two types of integrals:

Definite integral:
This type of Integral has a boundary within which given functions need to be calculated. It is
denoted as,
$\int_{a}^{b}{f\left( x \right).dx=F\left( x \right)}$

Indefinite integral:
This type of integral don’t have any specific boundary that means there is no upper limit and no lower limit. It can be denoted as,
$\int{f\left( x \right).dx}=F\left( x \right)+C$

Application of integration:
There are various application of integration as follows,
Area between curves
Distance, Velocity and Acceleration
Volume
Average value of a function
Surface area
Probability
Arc length

Note: AP calculus is the one of the most important branches of mathematics that deals with continuous change. Mainly calculus broadly divided into two parts i.e. differential calculus and integral calculus. Both of these deal with the function of a rate of a change. Both of these concepts based on the limits and continuity. AP calculus is a very vast topic which will need an ample amount of time to understand.