Question

How do you solve $\tan x=2.5$ ?

Answer 1

Hint : We explain the function ${{\tan }^{-1}}x$ . We express the inverse function of tan in the form of $arc\tan \left( x \right)={{\tan }^{-1}}x$ . We draw the graph of $arc\tan \left( x \right)$ and the line $x=2.5$ to find the intersection point. We can also solve it as $y=\tan x=2.5$ and find their intersection.

Complete step-by-step answer :
The given expression is the inverse function of trigonometric ratio tan. We need to find ${{\tan }^{-1}}\left( 2.5 \right)$ .
The arcus function represents the angle which on ratio tan gives the value.
Each of the trigonometric functions is periodic in the real part of its argument, running through all its values twice in each interval of $2\pi$ .
The general solution for that value where $\tan \alpha =x$ will be $n\pi +\alpha ,n\in \mathbb{Z}$ .
But for ${{\tan }^{-1}}x$ , we won’t find the general solution. We use the principal value. For ratio tan we have $-\dfrac{\pi }{2}\le {{\tan }^{-1}}x\le \dfrac{\pi }{2}$ .
The graph of the function is

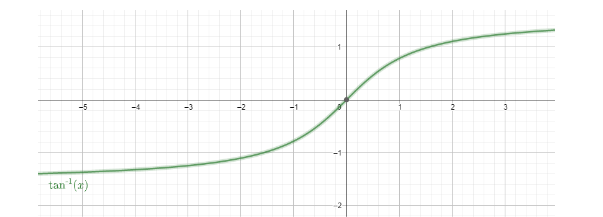
We now place the value of $x=2.5$ in the function of ${{\tan }^{-1}}x$ .
Let the angle be $\theta$ for which ${{\tan }^{-1}}\left( 2.5 \right)=\theta$ . This gives $\tan \theta =2.5$ .
For this we take the line of $x=2.5$ and see the intersection of the line with the graph ${{\tan }^{-1}}x$ .
Putting the value in the graph of ${{\tan }^{-1}}x$ , we get $\theta =68.2$ . (approx.)
We get the value of y coordinates as ${{68.2}^{\circ }}$ .
So, the correct answer is “ ${{68.2}^{\circ }}$ ”.

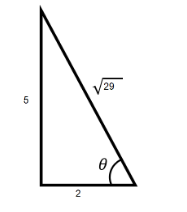
Note : We can also apply the trigonometric identity where $\tan \theta =2.5=\dfrac{5}{2}$ . We express it in a right-angle triangle whose height will be 5 and the base will be 2.

In that case the hypotenuse will be $\sqrt{{{5}^{2}}+{{2}^{2}}}=\sqrt{29}$ .

Also, in the exact solution domain of $-\dfrac{\pi }{2}\le \theta \le \dfrac{\pi }{2}$ , the solution is $\theta =68.2$ .