Question

How do you solve $\tan x = 0$ $?$

Answer 1

We need to know the trigonometric table values and the basic definition $\tan \theta$ .

To solve the given problem we need to find the values of $\theta$ . Also, we need to know the process of calculating the value of $\tan \theta$ the scientific calculator. We need to know the degree value $\pi$ . Also, we need to know the relation between $\sin \theta ,\cos \theta ,$ and $\tan\theta$ .

Complete step by step solution:
The given question is shown below,
$\tan x = 0$
We need to find the value $\theta$ from the above equation. Before that, we need to know the basic definition of $\tan \theta$ .
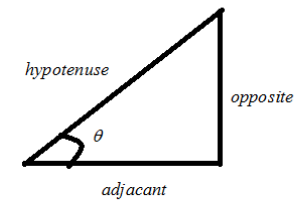
The above figure represents a triangle marked with the opposite side, adjacent side, and hypotenuse side according to the position of $\theta$ .
The above figure is used to represent the definition of $\sin \theta ,\cos \theta ,$ and $\tan \theta$ . Let’s see the definitions of $\sin \theta ,\cos\theta ,$ and $\tan \theta$ ,
$\sin \theta = \dfrac{{opposite}}{{hypotenuse}}$
$\cos \theta = \dfrac{{adjacant}}{{hypotenuse}}$
$\tan \theta = \dfrac{{opposite}}{{adjacant}}$
From the above three equations, we can define the $\tan \theta$ as follows,
$\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}$ $\to \left( A \right)$
We need to find the value of $\tan x = 0$ . So, we get
$x = \arctan \left( 0 \right)$
We know that,
$\sin \left( 0 \right) = 0$
$0 = \arcsin \left( 0 \right)$

\sin \left( \pi \right) = 0 \\\ \pi = \arcsin \left( 0 \right) \\\\$$ From the equation, $$\left( A \right)$$ we get when the value of $$\sin \theta $$ is $$0$$ , then automatically the value of $$\tan \theta $$ is $$0$$ $$(i.e\tan x = 0)$$ . So, we get

\tan \left( 0 \right) = 0 \\
0 = \arctan \left( 0 \right) \\
\tan \left( \pi \right) = 0 \\
\pi = \arctan \left( 0 \right) \\

So when $$\theta $$ the value is $$0,\pi ,2\pi ,3\pi ,......$$ the value of $$\tan \theta $$ becomes $$0$$ . **So, the final answer is, If $$\tan x = 0$$ , then the value of $$x = 0,\pi ,2\pi ,3\pi ,....$$ ** **Note:** In this type of question we would find the value of $$x$$ from the given equation. In this problem, we use trigonometric table values for finding the value of $$x$$ . Also, we can use a scientific calculator to find the value $$x$$ . On finding the $$x$$ value in the scientific calculator we can use radian mode or degree mode. If we want to find $$x$$ value in decimal we can use radian mode otherwise we can use degree mode.