Question

How do you solve $\sin x\left( \sin x+1 \right)=0$?

Answer 1

We know that if ab=0 then either a is equal to 0 or b is equal to 0 both will be the solution. So we can find 2 value of sin x and solve them separately to find the solution of the equation

Complete step by step answer;
The given equation is $\sin x\left( \sin x+1 \right)=0$
We know if a product of 2 numbers is 0 then at least one of them is 0. So if product of $\sin x$ and $\sin x+1$ is 0 then
$\sin x=0$ is one solution and $\sin x+1=0$ is another solution of the equation
First lets evaluate all possible x for $\sin x=0$ from graph

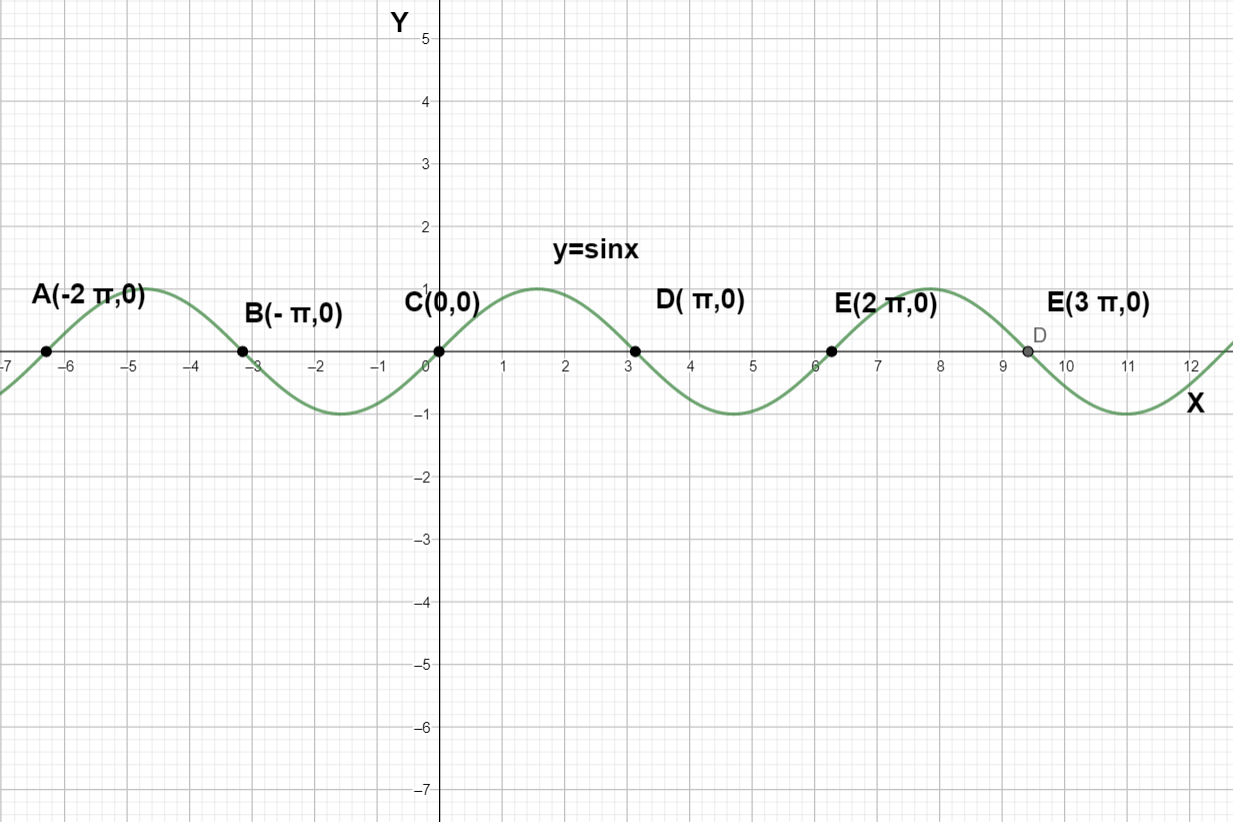
We can see that the solution for $\sin x=0$ is $x=n\pi$ where n is an integer n= …-1, 0, 1, 2, …..
Similarly we can find the solution the solution of $\sin x+1=0$ or sin x is equal to -1 form the graph

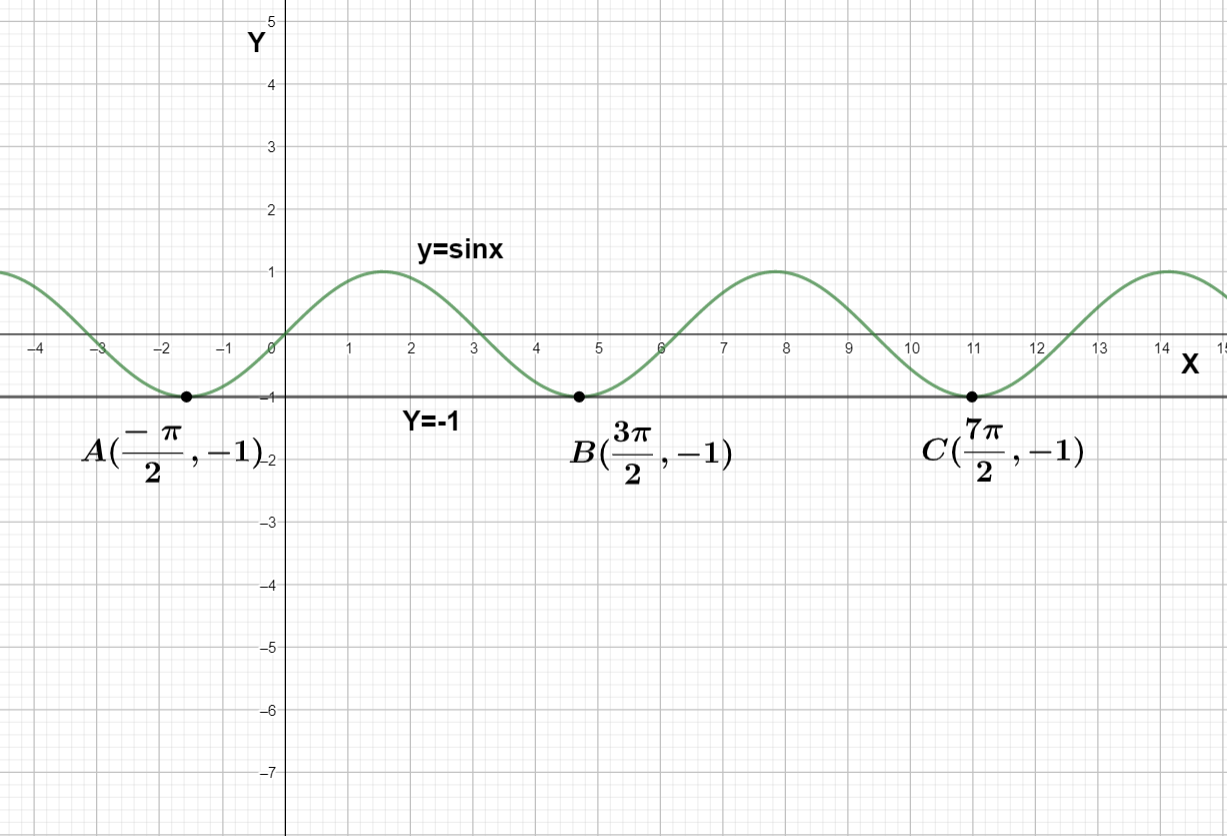
We can see that the solutions are $-\dfrac{\pi }{2}$ , $\dfrac{3\pi }{2}$ , $\dfrac{7\pi }{2}$
So we can generalize it by $\dfrac{\left( 4n+3 \right)\pi }{2}$ where n is an integer n= …-1, 0, 1, 2, ….

Note:
While solving these type of question where the variable in the polynomial equation is a trigonometric function or exponential function, do check the roots of the equation comes in the range of the function for example in the above question if one root sin x would 2 then we will not consider 2 as a root because we know sin x can never be equal to 2. Similarly in exponential function do check all roots are positive because range of exponential is positive real number.