Question

How do you solve $\sin \,x\, = \,\dfrac{1}{2}$?

Answer 1

For solving this particular question we can take help from the sine graph and find the given value just by observing. Also, we can find it by using the right angled triangle. In that case one can use the relation of sine function with the sides of the triangle.

Complete step by step solution:
The equation is $\sin \,x\, = \,\dfrac{1}{2}$
The solutions should be lying between$\,0^\circ \leqslant \,x \geqslant 360^\circ$. This means we are looking for all the angles, x, in this interval which have a sin of $\dfrac{1}{2}$. The curve for the function $\sin \,x$ for the given interval is:

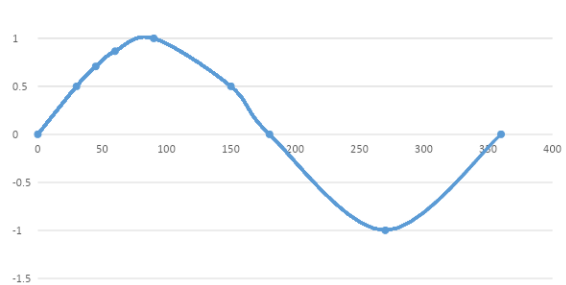
From the figure above we note that the angle with value equal to $\dfrac{1}{2}$ is 30°. Using this graph, we can conclude that all the angles which have a sin of$\dfrac{1}{2}$. All those angles are $x\, = \,30^\circ ,\,150^\circ$
So, within the given interval there are two solutions $x\, = \,30^\circ ,\,150^\circ$.
We can also find the values using a right triangle.
Using a right angled triangle, sine value is equal to the ratio of perpendicular and hypotenuse.
We know that, $\sin \,x\, = \,\dfrac{1}{2} = \dfrac{{perpendicular}}{{hypotenuse}}$
As we can see in the triangle, $\sin \left( {{{30}^\circ }} \right)$ has perpendicular and hypotenuse as 1 and 2 respectively. So,
$\Rightarrow \sin \left( {{{30}^\circ }} \right) = \dfrac{1}{2}$
So the correct answer is ${30^ \circ }$.

Note:
Observe the graph carefully before finding the conclusion. Also, one should know or refer to the table with exact values of all the trigonometric functions. This table is useful for all the trigonometric questions. The curve of the sine function is continuous but in this particular question we needed to find $\dfrac{1}{2}$ between the values of $\,0^\circ \leqslant \,x \geqslant 360^\circ$. Also, In case of right angled triangles, we can find it by using $\sin \, = \dfrac{{perpendicular}}{{{\text{Hypotenuse}}}}$.