Solveeit Logo
Login

Question

Question: How do you solve \[\sin \left( \alpha +\beta \right)\] when we are given \[\sin \alpha =\dfrac{12}{1...

How do you solve sin⁡(α+β)\sin \left( \alpha +\beta \right) when we are given sin⁡α=1213\sin \alpha =\dfrac{12}{13} and cos⁡β=−45?\cos \beta =\dfrac{-4}{5}?

Explanation

Solution

We are given the value of sin⁡α\sin \alpha and cos⁡β\cos \beta and we are asked to find the value of sin⁡(α+β).\sin \left( \alpha +\beta \right). To find the value of sin⁡(α+β)\sin \left( \alpha +\beta \right) we will first calculate the value of cos⁡α\cos \alpha and sin⁡β.\sin \beta . To do so we will need to knowledge of quadrant and the sign of sin and cos in these quadrants. After that, we will find the value of sin⁡(α+β).\sin \left( \alpha +\beta \right). We will use sin⁡(α+β)=sin⁡αcos⁡β+cos⁡αsin⁡β\sin \left( \alpha +\beta \right)=\sin \alpha \cos \beta +\cos \alpha \sin \beta to find the required value.

Complete step-by-step solution:
We are given sin⁡α=1213\sin \alpha =\dfrac{12}{13} and we have cos⁡β=−45.\cos \beta =\dfrac{-4}{5}. We are asked to find the value of sin⁡(α+β).\sin \left( \alpha +\beta \right). We know that sin⁡(α+β)\sin \left( \alpha +\beta \right) is given as sin⁡(α+β)=sin⁡αcos⁡β+cos⁡αsin⁡β.\sin \left( \alpha +\beta \right)=\sin \alpha \cos \beta +\cos \alpha \sin \beta . So to find the value of sin⁡(α+β)\sin \left( \alpha +\beta \right) we will first need to find the value of sin⁡β\sin \beta and cos⁡α.\cos \alpha . Now, to calculate these value, we will use the identity given as sin⁡2θ+cos⁡2θ=1.{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1. So, using this, we will find our value.
We will start with sin⁡α=1213.\sin \alpha =\dfrac{12}{13}. We have sin⁡α=1213.\sin \alpha =\dfrac{12}{13}. So using the identity sin⁡2α+cos⁡2α=1{{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1 and putting sin⁡α=1213\sin \alpha =\dfrac{12}{13} in the above equation, we get,
(1213)2+cos⁡2α=1{{\left( \dfrac{12}{13} \right)}^{2}}+{{\cos }^{2}}\alpha =1
So, we get,
⇒144169+cos⁡2α=1\Rightarrow \dfrac{144}{169}+{{\cos }^{2}}\alpha =1
On simplifying, we get,
⇒cos⁡α=1−144169=25169\Rightarrow \cos \alpha =1-\dfrac{144}{169}=\dfrac{25}{169}
So, we get,
⇒cos⁡α=±25169\Rightarrow \cos \alpha =\pm \sqrt{\dfrac{25}{169}}
As, 25=5\sqrt{25}=5 and 169=13,\sqrt{169}=13, so, we get,
⇒cos⁡α=±513\Rightarrow \cos \alpha =\pm \dfrac{5}{13}
So, we have that for sin⁡α=1213,\sin \alpha =\dfrac{12}{13}, we have cos⁡α=513\cos \alpha =\dfrac{5}{13} and also cos⁡α=−513.....(i)\cos \alpha =\dfrac{-5}{13}.....\left( i \right)
Now, we will use cos⁡β=−45\cos \beta =\dfrac{-4}{5} and we know that cos⁡2β+sin⁡2β=1.{{\cos }^{2}}\beta +{{\sin }^{2}}\beta =1. So, using cos⁡β=−45,\cos \beta =\dfrac{-4}{5}, we get,
⇒(−45)2+sin⁡2β=1\Rightarrow {{\left( \dfrac{-4}{5} \right)}^{2}}+{{\sin }^{2}}\beta =1
Simplifying, we will get,
⇒sin⁡2β=1−1625=925\Rightarrow {{\sin }^{2}}\beta =1-\dfrac{16}{25}=\dfrac{9}{25}
So, we get,
⇒sin⁡β=±35\Rightarrow \sin \beta =\pm \dfrac{3}{5}
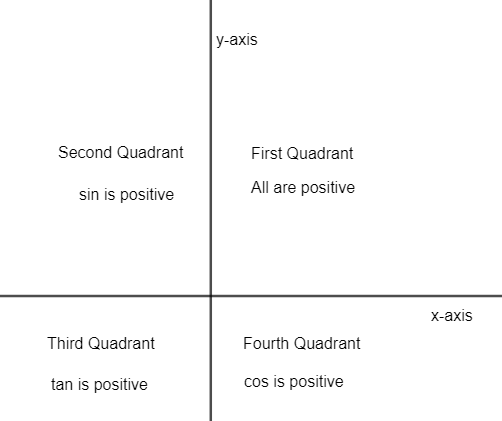
Now, cos⁡β=−45\cos \beta =\dfrac{-4}{5} is possible in the second quadrant and third quadrant and sin is positive as well as negative in these two quadrants. So, sin⁡β=+35\sin \beta =\dfrac{+3}{5} and sin⁡β=−35\sin \beta =\dfrac{-3}{5} and both are possible.
So, for cos⁡β=−45\cos \beta =\dfrac{-4}{5} we get, sin⁡β=35\sin \beta =\dfrac{3}{5} and sin⁡β=−35.....(ii)\sin \beta =\dfrac{-3}{5}.....\left( ii \right)
So, we get, for the set of values and we will list them as
A. sin⁡α=1213,cos⁡α=513,sin⁡β=35,cos⁡β=−45\text{A}\text{. }\sin \alpha =\dfrac{12}{13},\cos \alpha =\dfrac{5}{13},\sin \beta =\dfrac{3}{5},\cos \beta =\dfrac{-4}{5}
B. sin⁡α=1213,cos⁡α=−513,sin⁡β=35,cos⁡β=−45\text{B}\text{. }\sin \alpha =\dfrac{12}{13},\cos \alpha =\dfrac{-5}{13},\sin \beta =\dfrac{3}{5},\cos \beta =\dfrac{-4}{5}
C. sin⁡α=1213,cos⁡α=513,sin⁡β=−35,cos⁡β=−45\text{C}\text{. }\sin \alpha =\dfrac{12}{13},\cos \alpha =\dfrac{5}{13},\sin \beta =\dfrac{-3}{5},\cos \beta =\dfrac{-4}{5}
D. sin⁡α=1213,cos⁡α=−513,sin⁡β=−35,cos⁡β=−45\text{D}\text{. }\sin \alpha =\dfrac{12}{13},\cos \alpha =\dfrac{-5}{13},\sin \beta =\dfrac{-3}{5},\cos \beta =\dfrac{-4}{5}
Now we will use these values on the formula sin⁡(α+β)=sin⁡αcos⁡β+cos⁡αsin⁡β\sin \left( \alpha +\beta \right)=\sin \alpha \cos \beta +\cos \alpha \sin \beta and find our answer. We will use the value one by one.
a. For part A,
sin⁡(α+β)=1213×(−45)+513×35\sin \left( \alpha +\beta \right)=\dfrac{12}{13}\times \left( \dfrac{-4}{5} \right)+\dfrac{5}{13}\times \dfrac{3}{5}
So, we get,
⇒sin⁡(α+β)=−3365\Rightarrow \sin \left( \alpha +\beta \right)=\dfrac{-33}{65}
b. For part B,
sin⁡(α+β)=1213×(−45)+(−513)×35\sin \left( \alpha +\beta \right)=\dfrac{12}{13}\times \left( \dfrac{-4}{5} \right)+\left( \dfrac{-5}{13} \right)\times \dfrac{3}{5}
⇒sin⁡(α+β)=−6365\Rightarrow \sin \left( \alpha +\beta \right)=\dfrac{-63}{65}
c. For part C,
sin⁡(α+β)=1213×(−45)+(513)×(−35)\sin \left( \alpha +\beta \right)=\dfrac{12}{13}\times \left( \dfrac{-4}{5} \right)+\left( \dfrac{5}{13} \right)\times \left( \dfrac{-3}{5} \right)
⇒sin⁡(α+β)=−6365\Rightarrow \sin \left( \alpha +\beta \right)=\dfrac{-63}{65}
d. For part D,
sin⁡(α+β)=1213×(−45)+(−513)×(−35)\sin \left( \alpha +\beta \right)=\dfrac{12}{13}\times \left( \dfrac{-4}{5} \right)+\left( \dfrac{-5}{13} \right)\times \left( \dfrac{-3}{5} \right)
⇒sin⁡(α+β)=−3365\Rightarrow \sin \left( \alpha +\beta \right)=\dfrac{-33}{65}
Hence, we get two solutions. We have the value of sin⁡(α+β)\sin \left( \alpha +\beta \right) as −6365\dfrac{-63}{65} and sin⁡(α+β)\sin \left( \alpha +\beta \right) as −3365.\dfrac{-33}{65}.

Note: While solving the square root we need to be careful with the sign when we do root, it will give positive and negative values. We need to compare which out of the positive or negative is possible by checking the quadrant in which sin and cos are taking positive or negative values. We have a table showing sign as