Question

How do you solve quadratic inequality, graph and write in interval notation $- {x^2} - x + 6 < 0$?

Answer 1

We can see that the given curve indicates the curve parabola. Now, for the graph of a parabola, we need two main points. These two important points are y intercept and x intercept. Therefore, we will first find these two points and then find its interval by considering the parts less than zero which are below the x-axis.

Complete step by step solution:
We are given $- {x^2} - x + 6 < 0$.
We can write it as an equation of parabola $y = - {x^2} - x + 6$.
We will first find the y intercept of the graph. For this we will take $x = 0$.
$y = - {x^2} - x + 6 \\\ \Rightarrow y = 6 \\\$
Therefore, the y intercept of the graph is $\left( {0,6} \right)$.
Now, we will find the x intercept of the graph. For this we will take $y = 0$.

$$y = - {x^2} - x + 6 \\\ \Rightarrow 0 = - {x^2} - x + 6 \\\ \Rightarrow 0 = {x^2} + x - 6 \\\$$

For solving this, we will factories the polynomial ${x^2} + x - 6$ by splitting the middle term.
Therefore, we can write

$$\Rightarrow {x^2} + 3x - 2x - 6 = 0 \\\ \Rightarrow x\left( {x + 3} \right) - 2\left( {x + 3} \right) = 0 \\\ \Rightarrow \left( {x + 3} \right)\left( {x - 2} \right) = 0 \\\$$

$\Rightarrow x + 3 = 0 \\\ \Rightarrow x = - 3 \\\$ or $\Rightarrow x - 2 = 0 \\\ \Rightarrow x = 2 \\\$
Thus, we have two x intercepts for the given graph which are $\left( { - 3,0} \right)$ and $\left( {2,0} \right)$.
We will now decide the shape of the parabola.
In our equation, the coefficient of $x$ is $- 1$, Therefore the shape of the parabola will be downward like $\cap$.
From this we can say that $x < \- 3$ and $x > 2$ are the parts of the parabola which are below the x-axis.
Hence, in interval notation, we can write the inequality $- {x^2} - x + 6 < 0$ as $\left( { - \infty , - 3} \right) \cup \left( {2,\infty } \right)$.
If we plot the graph of this inequality, it can be indicated as the shaded portion as shown in this graph:

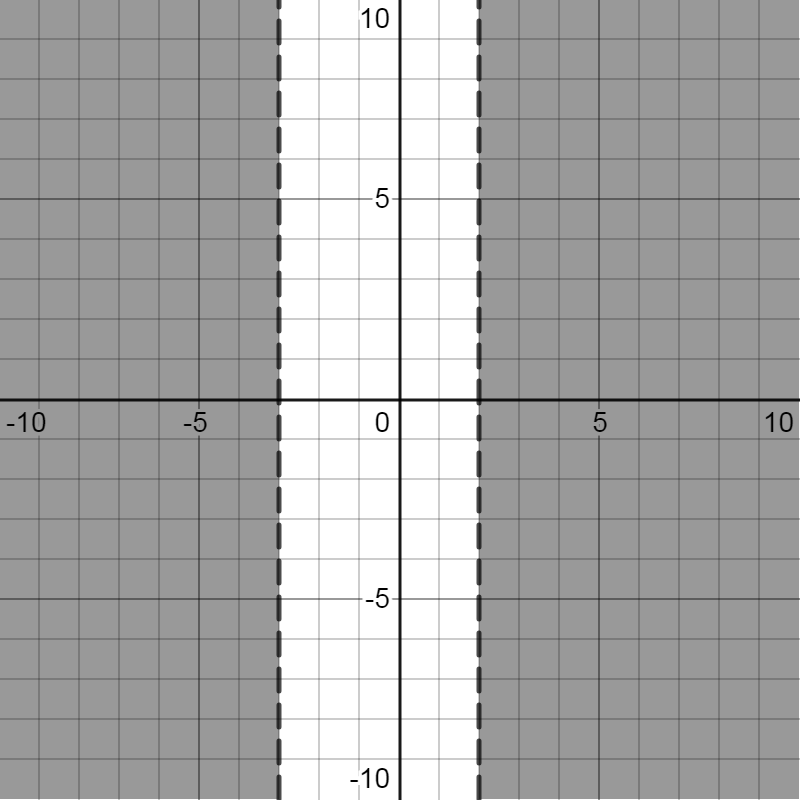
Note: Thus, in this type of equation when we are asked to write an inequality in the interval notation form, first we need to find the intercepts of both the axis of the curve. After that if the inequality is less than zero, then we have to consider parts of the curve below the x-axis. And if the inequality is greater than zero, then we have to consider parts of the curve above the x-axis.