Question

How do you solve $\left| y \right|=5$ ?

Answer 1

To solve the above given expression, we should know the concepts of absolute values and modulus. The modulus function, or the absolute value of a number implies that $\left| x \right|=x$ and is equal to $x$ if $x\ge 0$ or is equal to $-x$ if $x < 0$ .

Complete step-by-step answer:
Given the expression:
$\Rightarrow \left| y \right|=5$
In the given expression the value of $y$ can be greater than zero, that is, it can be a positive number, or it can also be lesser than zero indicating that it is a negative number.
Therefore, the expression can be simplified and also written as$y=\pm 5$ .
This equation or expression given above, also represents the equation of a line that is parallel to the $x$ - axis and passes through the point $y=5$ on the $y$ - axis. Since, the line is parallel to the horizontal or $x$ - axis, the slope of the line will be zero.
The slope-intercept form of the above line can be written as $y=0x+5$ , where $0$ represents the slope of the line and $5$ represents the constant in the equation of the line. The same concept will be applied to the graph of $y=-5$ as well.
The graph for the above equation $\left| y \right|=5$ can be represented as below,

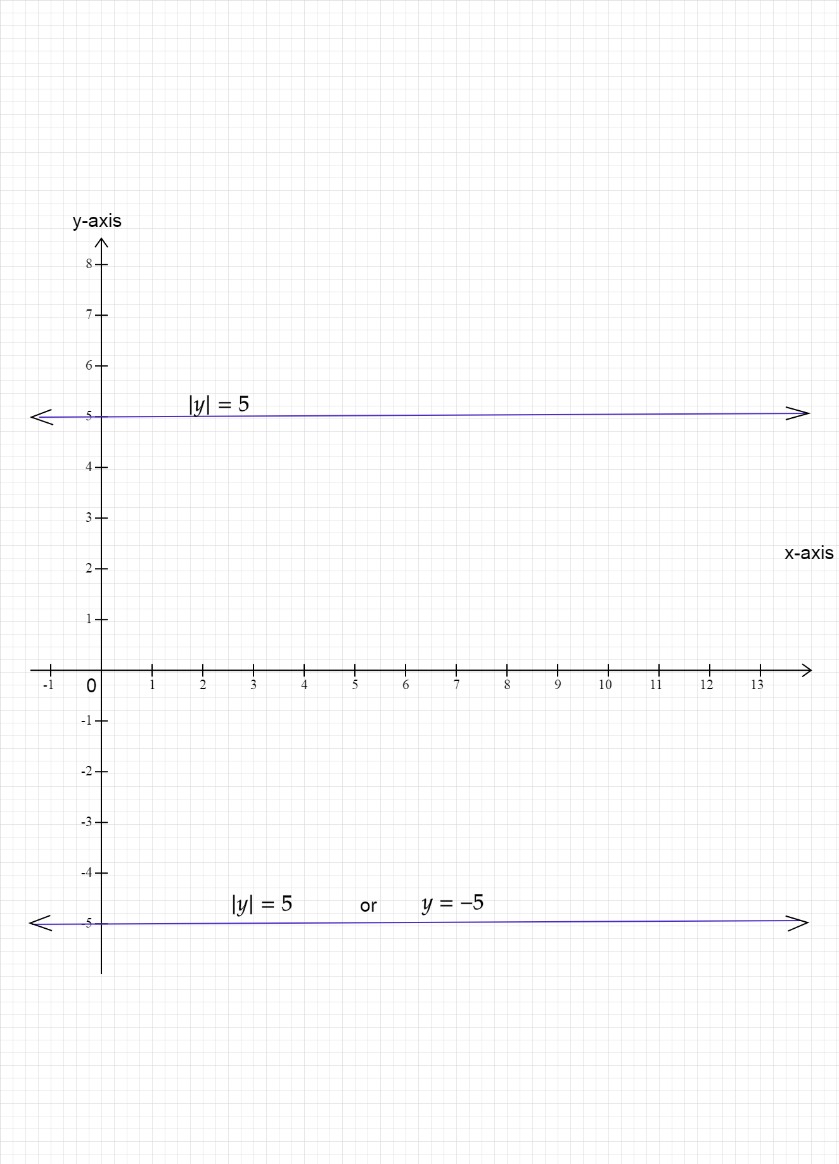
The graph can be plotted by taking and substituting different values of $x$ in the equation $y=0x+5$ and then calculating the respective values for $y$. For example, if we take $x=1$ and substitute the value in the given equation, we get,
$\Rightarrow y=0\left( 1 \right)+5$
On simplifying the above equation, we get the value of $y$ as,
$\Rightarrow y=5$
Similarly, we can take different values for $x$ and find the value for $y$.
In the same manner, we can also plot the graph for $y=0x-5$ or $y=-5$ by taking different values of $x$ and then finding the corresponding values for $y$.
Therefore, on solving$\left| y \right|=5$, we get$y=\pm 5$

Note: Absolute value of a number means how far the number is from zero on the number line. This also means that while finding the absolute value of a given number, we remove any negative sign in front of the number and take its positive value only.