Question

How do you solve $\left( {\tan x + 1} \right)\left( {\sin x - 1} \right) = 0$?

Answer 1

First, set both individual factors on the left side of the equation equal to $0$. Next, set the first factor equal to $0$ and solve for $x$ using trigonometric properties. Then, we will get all solutions of the given equation. Next, set the second factor equal to $0$ and take the inverse sine of both sides of the equation to extract $x$ from inside the sine. Then, we will get all solutions of the given equation.

Formula used:
$\tan \dfrac{\pi }{4} = 1$
$\tan \left( {\pi - x} \right) = - \tan x$
$\tan \left( {2\pi - x} \right) = - \sin x$

Complete step by step solution:
Given equation: $\left( {\tan x + 1} \right)\left( {\sin x - 1} \right) = 0$
We have to find all possible values of $x$ satisfying given equation.
Since, if any individual factor on the left side of the equation is equal to $0$, the entire expression will be equal to $0$.
$\tan x + 1 = 0$
$\sin x - 1 = 0$
So, set the first factor equal to $0$ and solve.
Set the first factor equal to $0$.
$\tan x + 1 = 0$
Subtract $1$ from both sides of the equation.
$\Rightarrow \tan x = - 1$…(i)
Now, using the property $\tan \left( {\pi - x} \right) = - \tan x$ and $\tan \dfrac{\pi }{4} = 1$ in equation (i).
$\Rightarrow \tan x = - \tan \dfrac{\pi }{4}$
$\Rightarrow \tan x = \tan \left( {\pi - \dfrac{\pi }{4}} \right)$
$\Rightarrow x = \dfrac{{3\pi }}{4}$
Now, using the property $\tan \left( {2\pi - x} \right) = - \sin x$ and $\tan \dfrac{\pi }{4} = 1$ in equation (i).
$\Rightarrow \tan x = - \tan \dfrac{\pi }{4}$
$\Rightarrow \tan x = \tan \left( {2\pi - \dfrac{\pi }{4}} \right)$
$\Rightarrow x = \dfrac{{7\pi }}{4}$
Since, the period of the $\tan x$ function is $\pi$ so values will repeat every $\pi$ radians in both directions.
$x = \dfrac{{3\pi }}{4} + n\pi ,\dfrac{{7\pi }}{4} + n\pi$, for any integer $n$.
Now, set the second factor equal to $0$.
$\sin x - 1 = 0$
Add $1$ to both sides of the equation.
$\Rightarrow \sin x = 1$…(ii)
Now, we will find the values of $x$ satisfying $\sin x = 1$.
So, take the inverse sine of both sides of the equation to extract $x$ from inside the sine.
$x = \arcsin \left( 1 \right)$
Since, the exact value of $\arcsin \left( 1 \right) = \dfrac{\pi }{2}$.
$\Rightarrow x = \dfrac{\pi }{2}$
Since, the sine function is positive in the first and second quadrants.
So, to find the second solution, subtract the reference angle from $\pi$ to find the solution in the second quadrant.
$x = \pi - \dfrac{\pi }{2}$
$\Rightarrow x = \dfrac{\pi }{2}$
Since, the period of the $\sin x$ function is $2\pi$ so values will repeat every $2\pi$ radians in both directions.
$x = \dfrac{\pi }{2} + 2n\pi$, for any integer $n$.

Hence, $x = \dfrac{{3\pi }}{4} + n\pi ,\dfrac{{7\pi }}{4} + n\pi ,\dfrac{\pi }{2} + 2n\pi$, for any integer $n$ are solutions of the given equation.

Note: In above question, we can find the solutions of given equation by plotting the equation, $\left( {\tan x + 1} \right)\left( {\sin x - 1} \right) = 0$ on graph paper and determine all its solutions.

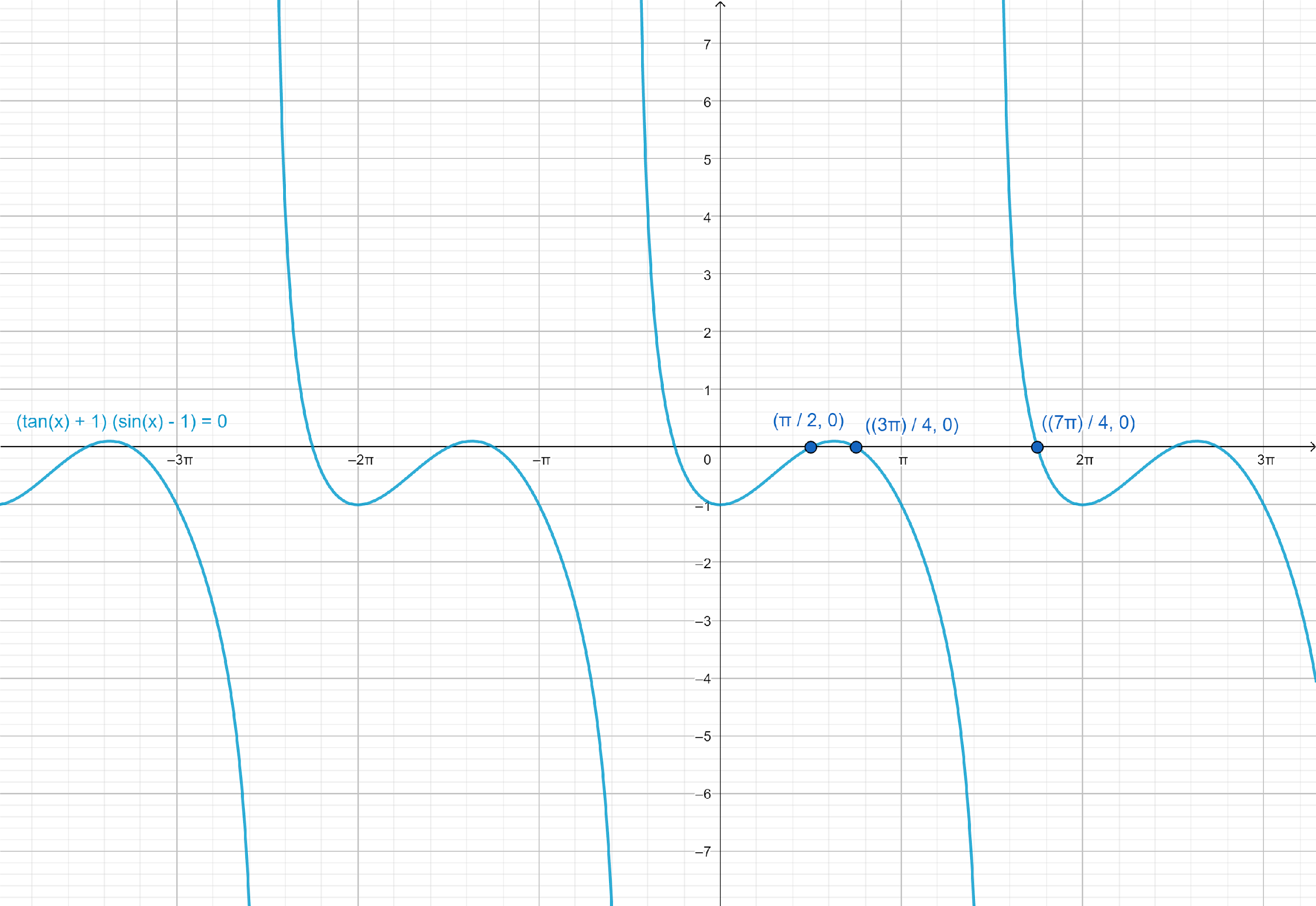
From the graph paper, we can see that $x = \dfrac{{3\pi }}{4}$, $x = \dfrac{{7\pi }}{4}$ and $x = \dfrac{\pi }{2}$ are solution of given equation, and solution repeat every $2\pi$ radians in both directions.
So, these will be the solutions of the given equation.
Final solution: Hence, $x = \dfrac{{3\pi }}{4} + n\pi ,\dfrac{{7\pi }}{4} + n\pi ,\dfrac{\pi }{2} + 2n\pi$, for any integer $n$are solutions of the given equation.