Solveeit Logo
Login

Question

Question: How do you solve \(\left| {\sin x} \right| = \dfrac{{\sqrt 3 }}{2}\) in the interval \(\left[ {0,{{3...

How do you solve ∣sin⁡x∣=32\left| {\sin x} \right| = \dfrac{{\sqrt 3 }}{2} in the interval [0,360∘]\left[ {0,{{360}^ \circ }} \right]?

Explanation

Solution

First, find the values of xx satisfying sin⁡x=32\sin x = \dfrac{{\sqrt 3 }}{2} using trigonometric properties.
Next, find the values of xx satisfying sin⁡x=−32\sin x = - \dfrac{{\sqrt 3 }}{2} using trigonometric properties. Next, find all values of xx in the interval [0,360∘]\left[ {0,{{360}^ \circ }} \right]. Then, we will get all solutions of the given equation in the given interval.

Formula used:

  1. sin⁡π3=32\sin \dfrac{\pi }{3} = \dfrac{{\sqrt 3 }}{2}
  2. sin⁡(π+x)=−sin⁡x\sin \left( {\pi + x} \right) = - \sin x
  3. sin⁡(2π−x)=−sin⁡x\sin \left( {2\pi - x} \right) = - \sin x

Complete step by step solution:
Given equation: ∣sin⁡x∣=32\left| {\sin x} \right| = \dfrac{{\sqrt 3 }}{2}
We have to find all possible values of xx satisfying given equation in the interval [0,360∘]\left[ {0,{{360}^ \circ }} \right].
First, we will find the values of xx satisfying sin⁡x=32\sin x = \dfrac{{\sqrt 3 }}{2}.
So, take the inverse sine of both sides of the equation to extract xx from inside the sine.
x=arcsin⁡(32)x = \arcsin \left( {\dfrac{{\sqrt 3 }}{2}} \right)
Since, the exact value of arcsin⁡(32)=π3\arcsin \left( {\dfrac{{\sqrt 3 }}{2}} \right) = \dfrac{\pi }{3}.
⇒x=π3\Rightarrow x = \dfrac{\pi }{3}
Since, the sine function is positive in the first and second quadrants.
So, to find the second solution, subtract the reference angle from π\pi to find the solution in the second quadrant.
x=π−π3x = \pi - \dfrac{\pi }{3}
⇒x=2π3\Rightarrow x = \dfrac{{2\pi }}{3}
Since, the period of the sin⁡x\sin x function is 2π2\pi so values will repeat every 2π2\pi radians in both directions.
x=π3+2nπ,2π3+2nπx = \dfrac{\pi }{3} + 2n\pi ,\dfrac{{2\pi }}{3} + 2n\pi , for any integer nn.
Now, we will find the values of xx satisfying sin⁡x=−32\sin x = - \dfrac{{\sqrt 3 }}{2}…(i)
So, using the property sin⁡(π+x)=−sin⁡x\sin \left( {\pi + x} \right) = - \sin x and sin⁡π3=32\sin \dfrac{\pi }{3} = \dfrac{{\sqrt 3 }}{2} in equation (i).
⇒sin⁡x=−sin⁡π3\Rightarrow \sin x = - \sin \dfrac{\pi }{3}
⇒sin⁡x=sin⁡(π+π3)\Rightarrow \sin x = \sin \left( {\pi + \dfrac{\pi }{3}} \right)
⇒x=4π3\Rightarrow x = \dfrac{{4\pi }}{3}
Now, using the property sin⁡(2π−x)=−sin⁡x\sin \left( {2\pi - x} \right) = - \sin x and sin⁡π3=32\sin \dfrac{\pi }{3} = \dfrac{{\sqrt 3 }}{2} in equation (i).
⇒sin⁡x=−sin⁡π3\Rightarrow \sin x = - \sin \dfrac{\pi }{3}
⇒sin⁡x=sin⁡(2π−π3)\Rightarrow \sin x = \sin \left( {2\pi - \dfrac{\pi }{3}} \right)
⇒x=5π3\Rightarrow x = \dfrac{{5\pi }}{3}
Since, the period of the sin⁡x\sin x function is 2π2\pi so values will repeat every 2π2\pi radians in both directions.
x=4π3+2nπ,5π3+2nπx = \dfrac{{4\pi }}{3} + 2n\pi ,\dfrac{{5\pi }}{3} + 2n\pi , for any integer nn.
Now, find all values of xx in the interval [0,360∘]\left[ {0,{{360}^ \circ }} \right].
Since, it is given that x∈[0,360∘]x \in \left[ {0,{{360}^ \circ }} \right], hence put n=0n = 0 in the general solution.
So, putting n=0n = 0 in x=π3+2nπ,2π3+2nπx = \dfrac{\pi }{3} + 2n\pi ,\dfrac{{2\pi }}{3} + 2n\pi , we get
x=π3,2π3x = \dfrac{\pi }{3},\dfrac{{2\pi }}{3}
Now, putting n=0n = 0 in x=4π3+2nπ,5π3+2nπx = \dfrac{{4\pi }}{3} + 2n\pi ,\dfrac{{5\pi }}{3} + 2n\pi ,we get
x=4π3,5π3x = \dfrac{{4\pi }}{3},\dfrac{{5\pi }}{3}
Thus, x=π3,2π3,4π3,5π3x = \dfrac{\pi }{3},\dfrac{{2\pi }}{3},\dfrac{{4\pi }}{3},\dfrac{{5\pi }}{3} or x=60∘,120∘,240∘,300∘x = {60^ \circ },{120^ \circ },{240^ \circ },{300^ \circ }.

Final solution: Hence, x=π3,2π3,4π3,5π3x = \dfrac{\pi }{3},\dfrac{{2\pi }}{3},\dfrac{{4\pi }}{3},\dfrac{{5\pi }}{3} or x=60∘,120∘,240∘,300∘x = {60^ \circ },{120^ \circ },{240^ \circ },{300^ \circ } are solutions of the given equation in the interval [0,360∘]\left[ {0,{{360}^ \circ }} \right].

Note:
In above question, we can find the solutions of given equation by plotting the equation, ∣sin⁡x∣=32\left| {\sin x} \right| = \dfrac{{\sqrt 3 }}{2} on graph paper and determine all solutions which lie in the interval, [0,360∘]\left[ {0,{{360}^ \circ }} \right].

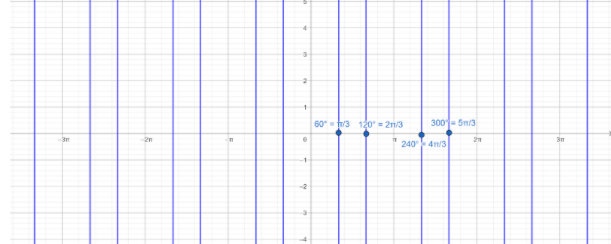
From the graph paper, we can see that there are four values of xx in the interval [0,360∘]\left[ {0,{{360}^ \circ }} \right].
So, these will be the solutions of the given equation in the given interval.
Final solution: Hence, x=π3,2π3,4π3,5π3x = \dfrac{\pi }{3},\dfrac{{2\pi }}{3},\dfrac{{4\pi }}{3},\dfrac{{5\pi }}{3} or x=60∘,120∘,240∘,300∘x = {60^ \circ },{120^ \circ },{240^ \circ },{300^ \circ } are solutions of the given equation in the interval [0,360∘]\left[ {0,{{360}^ \circ }} \right].