Question
Question: How do you solve \(\left| {\dfrac{5}{{2x - 1}}} \right| \geqslant \left| {\dfrac{1}{{x - 2}}} \right...
How do you solve 2x−15⩾x−21?
Solution
The given inequality is in modulus function, it can be solved by taking different cases for domain of the given modulus functions so that we can open it with positive or negative sign accordingly, then solve for all the cases and finally take the union of all results.
Modulus function can be understood as following:
\left| x \right| = \left\\{ {\begin{array}{*{20}{c}}
x&{{\text{if}}\;x > 0} \\\
{ - x}&{{\text{if}}\,x < 0}
\end{array}} \right\\}
Complete step by step answer:
To solve the inequation 2x−15⩾x−21 we have to take different cases for domain of the function
To get the cases we will compare variables separately with zero,
⇒2x−1=0andx−2=0 ⇒x=21andx=2
x=21andx=2 Can’t be in domain because inequality is undefined for them, i.e. 01
There are three cases forming
Case I:
When x∈(−∞,21), where
∣2x−1∣=−(2x−1)=−2x+1=1−2x ∣x−2∣=−(x−2)=−x+2=2−x
∴ inequality will be written as
⇒2x−15⩾x−21 ⇒1−2x5⩾2−x1 ⇒1−2x5⩾2−x1 ⇒1−2x5−2−x1⩾0 ⇒(1−2x)(2−x)5(2−x)−1(1−2x)⩾0 ⇒(1−2x)(2−x)10−5x−1+2x⩾0 ⇒(1−2x)(2−x)9−3x⩾0 ⇒(1−2x)(2−x)3(3−x)⩾0 ⇒(1−2x)(2−x)(3−x)⩾0
Now, we will compare variable terms with zero to find values for x, then plot them on number line to check which interval is satisfying the condition.
⇒3−x=0,1−2x=0and2−x=0 ⇒x=3,x=21andx=2
Plotting them on a number line,
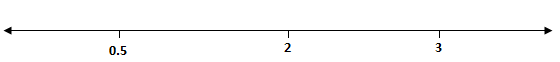
Take value of x from any interval and check which sign it is giving (+)or(−), then put the sign on that interval and alternative sign on its alternative intervals,
Checking for x=0which∈(−∞,21)
⇒(1−2x)(2−x)(3−x)⩾0 ⇒(1−2×0)(2−0)(3−0)⩾0 ⇒(1)(2)(3)⩾0 ⇒23⩾0
∴ putting the (+)and(−) signs alternatively
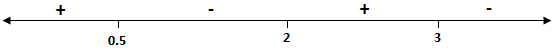
⇒x∈(−∞,21)∪(2,3]∩(−∞,21)
∵ case is x∈(−∞,21)
∴x∈(−∞,21) is the solution for this case
Case II:
x∈(21,2), then
∣2x−1∣=(2x−1)=2x−1 ∣x−2∣=−(x−2)=−x+2=2−x
∴ inequality will be written as
⇒2x−15⩾x−21 ⇒2x−15⩾2−x1 ⇒2x−15⩾2−x1 ⇒2x−15+x−21⩾0 ⇒(2x−1)(x−2)5(x−2)+1(2x−1)⩾0 ⇒(2x−1)(x−2)5x−10+2x−1⩾0 ⇒(2x−1)(x−2)(7x−11)⩾0
Again doing similar steps as case I,
⇒7x−11=0,2x−1=0andx−2=0 ⇒x=711,x=21andx=2
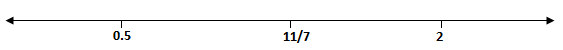
Checking for x=0which∈(−∞,21)
This is not true, so putting the signs accordingly
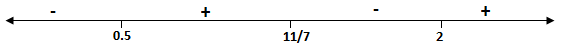
⇒x∈(21,711]∪(2,∞)∩(21,2)
∵ case is x∈(21,2)
∴x∈(21,711] is the solution for this case
Case III:
x∈(2,∞), then
∣2x−1∣=(2x−1)=2x−1 ∣x−2∣=(x−2)=x−2
∴ inequality will be written as
⇒2x−15⩾x−21 ⇒2x−15⩾x−21 ⇒2x−15⩾x−21 ⇒2x−15−x−21⩾0 ⇒(2x−1)(x−2)5(x−2)−1(2x−1)⩾0 ⇒(2x−1)(x−2)5x−10−2x+1⩾0 ⇒(2x−1)(x−2)(3x−9)⩾0 ⇒(2x−1)(x−2)3(x−3)⩾0 ⇒(2x−1)(x−2)(x−3)⩾0
Doing similar steps,
⇒x−3=0,2x−1=0andx−2=0 ⇒x=3,x=21andx=2
Checking for x=0which∈(−∞,21)
This is not true, so putting the signs accordingly

⇒x∈(21,2)∪[3,∞)∩(2,∞)
∵ case is x∈(2,∞)
∴x∈[3,∞) is the solution for this case
For final solution taking union of all results
⇒x∈(−∞,21)∪(21,711]∪[3,∞) is the final solution
Note: Square brackets stand for the including the number and parentheses stand for excluding the number. One can put alternative signs on the number line only when the degree of all the terms is 1. We have excluded −∞and∞ because they doesn’t exist physically.
