Question

How do you solve it $\tan \theta = \dfrac{5}{9}$ ?

Answer 1

Hint : We need to know the basic formula for $\tan \theta$ the involvement of the opposite side and adjacent side to solve the given problem. First, we need to find the value of $\theta$ . The given question involves the operation of addition/ subtraction/ multiplication/ division. Also, we need to know how to calculate the value ${\tan ^{ - 1}}$ in the calculator. While calculating ${\tan ^{ - 1}}$ the value we need to know which mode to be selected in the calculator.

Complete step-by-step answer :
The given question is shown below,
$\tan \theta = \dfrac{5}{9}$ ?
We need to find the value $\theta$ in the above equation. Before that, we need to know the basic definition of $\tan \theta$

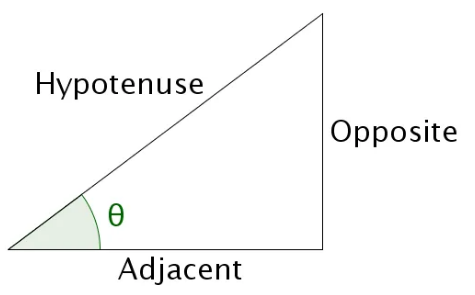
From the figure, we get that,
$\tan \theta = \dfrac{{opposite}}{{adjacent}}$ $\to \left( 1 \right)$
The given equation in the question is,
$\tan \theta = \dfrac{5}{9}$ $\to \left( 2 \right)$
By comparing the above two equations we get which is the value of the opposite side and which is the value of the adjacent side.
When the term $\tan$ is moved from the left side to the right side of the equation, it converts into ${\tan ^{ - 1}}$ . So, we get
$\tan \theta = \dfrac{5}{9}$
$\theta = {\tan ^{ - 1}}\left( {\dfrac{5}{9}} \right) \to \left( 3 \right)$
Let’s simplify the fractional term present in the above equation,
$\dfrac{5}{9} = 0.556 \to \left( 4 \right)$
Let’s substitute the equation $(4)$ in the equation $(3)$ , we get
$\theta = {\tan ^{ - 1}}\left( {0.556} \right)$
By calculating ${\tan ^{ - 1}}\left( {0.556} \right)$ in the calculator in degree mode we get,
$\theta = 29.07$
So, the correct answer is “ $\theta = 29.07$ ”.

Note : After confirming that, we would find the value of $\theta$ in the given question. On finding the $\theta$ value we can use either radian mode or degree mode. If we want to find the value $\theta$ in decimal value, we can use radian mode in the calculator. If we want to find the value of $\theta$ in degrees, we can use degree mode in the calculator. Also, note that when” $\tan$ ” is the move from the left side to the right side of the equation it converts into ${\tan ^{ - 1}}$ .