Question

How do you solve for y in $3x+2y-6=0$?

Answer 1

We are given a linear equation in 2 variables, x and y. in order to solve for y, we shall transpose terms and express the equation in terms of y. Then, we will find two points on the equation to plot them on the XY-plane graph and join those points to find the graph of this equation.

Complete step-by-step solution:
We will put the values of x and y equal to zero one by one to find two simple points one of which will have its x-coordinate equal to zero and the other one would have its y-coordinate equal to zero.
We shall first find the points lying on the line whose equation is given by, $3x+2y-6=0$.
$\begin{aligned} & 2y=-3x+6 \\\ & \Rightarrow y=-\dfrac{3}{2}x+3 \\\ \end{aligned}$
Putting $x=0$ in the equation, we get
$3\left( 0 \right)+2y-6=0$
$\Rightarrow 2y-6=0$
Now, we shall transpose -6 to the right-hand side:
$\Rightarrow 2y=6$
Dividing both sides by 2, we get
$\Rightarrow y=\dfrac{6}{2}$
$\therefore y=3$
Therefore, we get the point as (0,3).
Putting $y=0$ in the equation, we get
$3x+2\left( 0 \right)-6=0$
$\Rightarrow 3x-6=0$
Now, we shall transpose -6 to the right-hand side:
$\Rightarrow 3x=6$
Dividing both sides by 3, we get
$\Rightarrow x=\dfrac{6}{3}$
$\therefore x=2$
Therefore, we get the point as (2,0).
Hence, the points are (0,3) and (2,0).

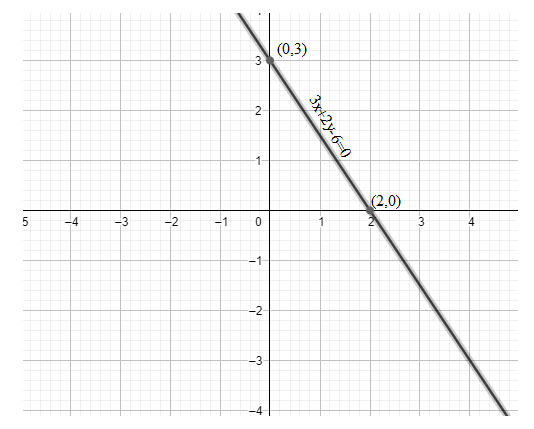
Note: While plotting the graph, the points must be carefully marked. For example, we sometimes tend to get confused between the two coordinates and mark (0,3) as (3,0). Also, while sketching any graph, the two points should always be taken such that the x or y coordinate is zero in them because it makes the calculations easier.