Solveeit Logo
Login

Question

Question: How do you solve for \(x\in \mathbb{R}\) the equation \(x!={{e}^{x}}?\)...

How do you solve for x∈Rx\in \mathbb{R} the equation x!=ex?x!={{e}^{x}}?

Explanation

Solution

This type of question can be best solved by using the graphical approach. All we need to do is to plot the two functions individually. After plotting them, we need to find an intersection point for the two curves. This gives us the value or the solution for the given equation.

Complete step by step solution:
Let us consider the given equation x!=ex.x!={{e}^{x}}. We now use the graphical method to solve for the value of x. In order to do so, we need to plot the graph for each side of the equation individually and see where the curves intersect each other. The x values for the location of these points gives us the solution to the equation.
For the given equation, let us consider f(x)=x!f\left( x \right)=x! and g(x)=ex.g\left( x \right)={{e}^{x}}.
We now plot the graph for the first function f(x)=x!f\left( x \right)=x! using any graphing tool or a graphing calculator. As shown in the figure below, we get the plot for this function as indicated by the green curve.
Next, we plot the graph for the second function g(x)=exg\left( x \right)={{e}^{x}} in a similar manner. The plot for this function is indicated by the grey curve drawn in the figure below.

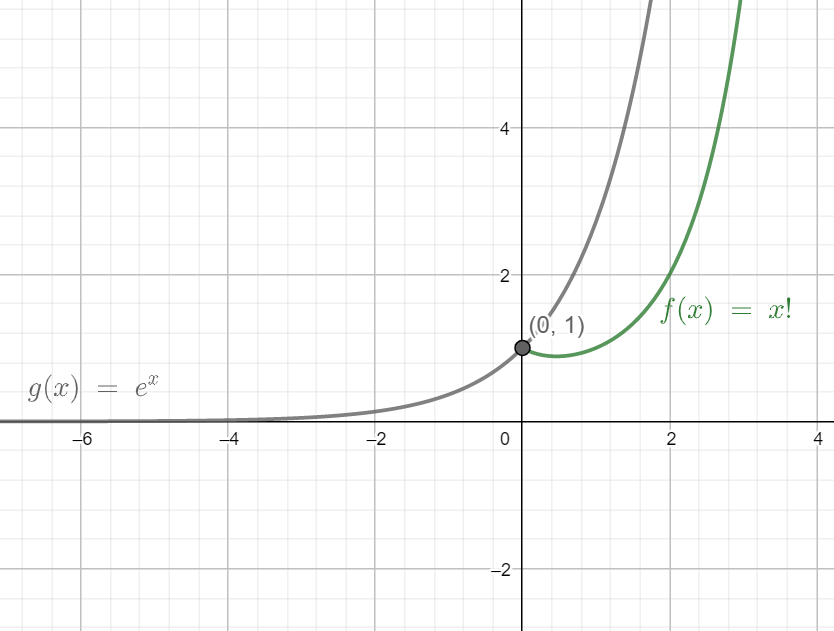
Next, we look for points of intersection of the two curves. We find a point (0,1)\left( 0,1 \right) at the intersection of the two curves. This means that the point (0,1)\left( 0,1 \right) is a solution to both the curves. This x value or x coordinate for this intersection point represents the solution to the equation x!=ex.x!={{e}^{x}}. We can see that x=0 at this point, so the only solution to this equation is x=0.
Hence, the solution to the equation x!=exx!={{e}^{x}} is x=0.

Note: While solving this question, the students need to be careful while considering the solution to the above equation. If we consider the y coordinate as the solution to this equation, it will not satisfy the equation given in the question and will lead to a wrong answer. Therefore, while getting the solution for two curves, the x coordinate is the one that represents the solution to the equation. The only exception is when the equation is a function of two variables, in which case we consider both x and y points as a part of the solution.