Question

How do you solve $\cos x = \dfrac{1}{2}$ ?

Answer 1

In the given question, we have to solve for $x$ , usually cosine function is having positive values in first and the fourth quadrants, so we will get two values for $x$ , by taking inverse cosine on both side we can find the value of $x$ .

Complete step-by-step answer:
Since in the given question the cosine value is greater than zero the value of $x$ will be in the first or fourth quadrant. The quadrant details for cosine function is given as in the below diagram

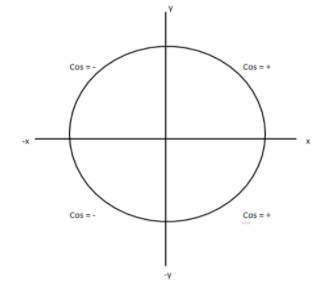
As they have not mentioned which quadrant values are to be determined we will find both the values.
Angle in first quadrant:
In order to find the value of $x$ take the cosine function to right hand side so that it will become inverse cosine function, which can be written as
$x = {\cos ^{ - 1}}\left( {\dfrac{1}{2}} \right)$
$\Rightarrow x = \dfrac{\pi }{3}$ This is the value of $x$ with respect to the first quadrant.
In order to find the value of $x$ with respect to fourth quadrant we can write the value of $x$ as $360$ minus tita, here tita $(\theta )$ is nothing but the value of $x$ ,
Therefore, $x = \left( {2\pi - \dfrac{\pi }{3}} \right)$
Taking L.C.M we can write as
$\Rightarrow x = \left( {\dfrac{{6\pi - \pi }}{3}} \right)$
Therefore on subtraction, we get the value of $x$ as
$\Rightarrow x = \left( {\dfrac{{5\pi }}{3}} \right)$
Hence $x = \dfrac{\pi }{3},\dfrac{{5\pi }}{3}$.

Note: Whenever we have this type of problem you need to know about quadrants first, so that we can find the values according to the quadrants. Sometimes if they give values less than zero or negative values then the quadrant will change and you need to calculate the values according to that.