Question

How do you solve $\cos x = 0$?

Answer 1

Here we need to find the solution of the given trigonometric equation. For that, we will use the unit circle, and then we will use the basic trigonometric ratios inside that unit circle. Then we will use the given value of the cosine function there and at last, we will find the general solution of the given trigonometric equation.

Complete step by step solution:
Here we need to find the solution of the given trigonometric equation i.e. $\cos x = 0$.
We know that the cosine function is defined as the ratio of the adjacent side to the hypotenuse.
Now, we will draw the unit circle with center $O$. We know that the circumference of the unit circle is equal to $2\pi$.

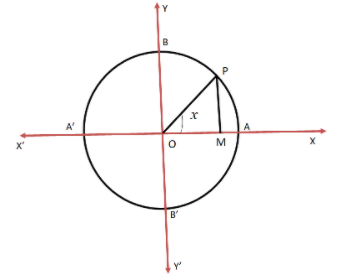
Now, we will consider the triangle $OPM$ and it is clear that;
$\Rightarrow \cos x = \dfrac{{OM}}{{OP}}$
It is given that $\cos x = 0$, so we will substitute the value zero here.
$\Rightarrow 0 = \dfrac{{OM}}{{OP}} \\\ \Rightarrow OM = 0 \\\$
We can clearly see that when $OM = 0$ then the final arm $OP$ of the angle $x$ coincides with $OY$ or $OY'$.
Similarly, the final arm $OP$ coincides with $OY$ or $OY'$ when $x = \dfrac{\pi }{2},\dfrac{{3\pi }}{2},\dfrac{{5\pi }}{2},\dfrac{{7\pi }}{2},......, - \dfrac{\pi }{2}, - \dfrac{{3\pi }}{2}, - \dfrac{{5\pi }}{2}, - \dfrac{{7\pi }}{2}$ i.e. when angle $x$ is an odd multiple of $\dfrac{\pi }{2}$ i.e. when $x = \left( {2n + 1} \right)\dfrac{\pi }{2}$ when $n \in Z$ is the solution of the given trigonometric equation.

Note:
Here we have obtained the solution of the given trigonometric equations. Trigonometric equations are defined as the equation which involves the trigonometric functions with angles as the variables. Also, we need to remember that trigonometric identities are defined as the equalities which include the trigonometric functions. They are always true for every value of the occurring variables where both sides of the equality are well defined. The cosine function is an even function, whereas the sine function is an odd function.