Question

How do you solve $\cos \left( \pi x \right)=0.5$ between the interval $0\le x<2$?

Answer 1

This question is from the topic of trigonometry. In this question, we have to find the value of x. In solving this question, we will first know that at what range of x, the value of cosx will be positive. After that, we will know at what values of x, the value of $\cos \left( \pi x \right)=0.5$.

Complete step by step solution:
Let us solve this question.
In this question, we have asked to find the values of x from the given equation. The given equation is $\cos \left( \pi x \right)=0.5$. As the range of x is given as $0\le x<2$, so we will have to find the value of x in this range.
Let us first understand that at what values of x, the value of $\cos \left( \pi x \right)$ will be positive.
Let us understand this from the following figure:

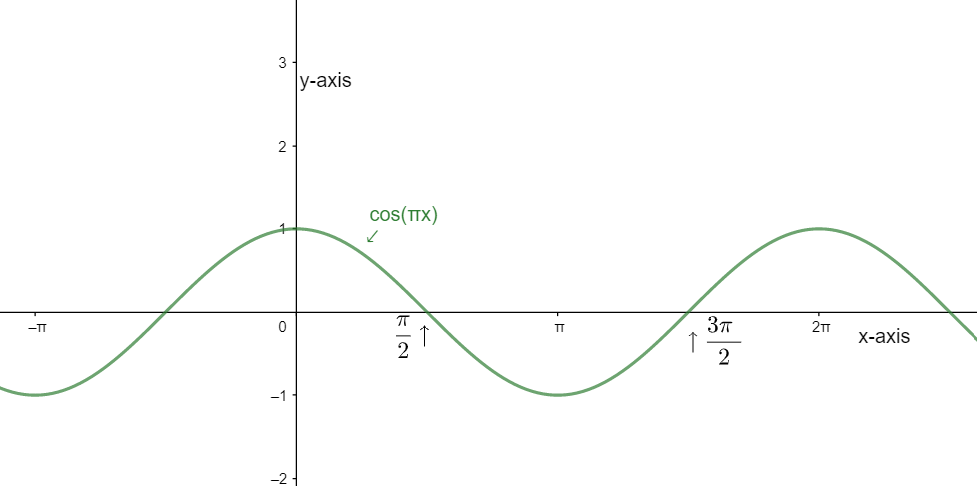
From the above figure, we can see that $\cos \left( \pi x \right)$ is positive in
$0\le \pi x<\dfrac{\pi }{2}$ and $\dfrac{3\pi }{2}<\pi x\le 2\pi$.
We can write the above range as
$0\le x<\dfrac{1}{2}$ and $\dfrac{3}{2}$ < $x \le 2$
We will only take the range of x as $0\le x<2$ because it is given in the question.
Now, let us know that where the value of $\cos \left( \pi x \right)$ is 0.5
$\cos \left( \pi x \right)=0.5$
We can write the above as
$co{{s}^{-1}}\left( \cos \left( \pi x \right) \right)=co{{s}^{-1}}\left( 0.5 \right)$
The above can also be written as
$\Rightarrow \pi x=co{{s}^{-1}}\left( 0.5 \right)$
We know that the value of $co{{s}^{-1}}\left( 0.5 \right)$ is $\dfrac{\pi }{3}$ and $\dfrac{5\pi }{3}$ in the range of $\left[ 0,2\pi \right]$. We can see from the following figure:

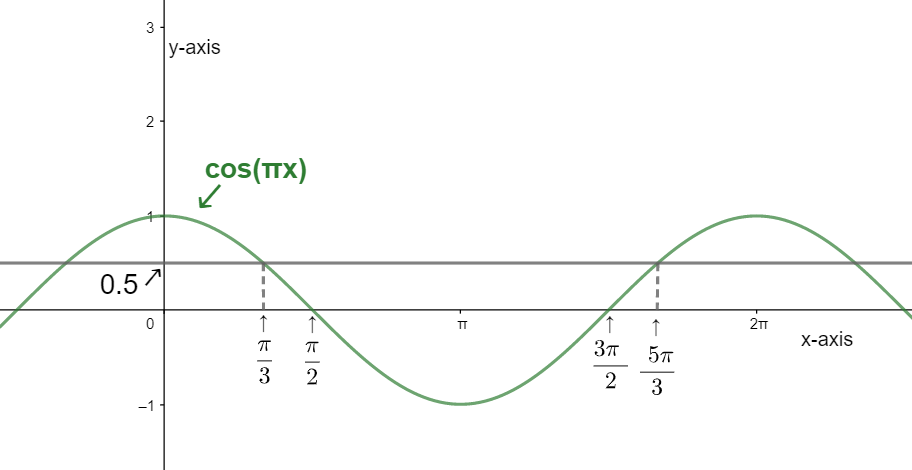
From the above figure, we can say that the value of 0.5 is at the points $\dfrac{\pi }{3}$ and $\dfrac{5\pi }{3}$.
So, we can say that
$\pi x=\dfrac{\pi }{3}$ and $\pi x=\dfrac{5\pi }{3}$
Or, we can say that
$x=\dfrac{1}{3}$ and $x=\dfrac{5}{3}$
So, we get that the values of x for the interval $0\le x<2$ are $\dfrac{1}{3}$ and $\dfrac{5}{3}$.

Note: We should have a better knowledge in the topic of trigonometry to solve this type of question easily. We should know the value of $co{{s}^{-1}}\left( 0.5 \right)$ in radian between the range $\left[ 0,2\pi \right]$. The values of $co{{s}^{-1}}\left( 0.5 \right)$ between that range are $\dfrac{\pi }{3}$ and $\dfrac{5\pi }{3}$. We should know the graph of function cos, as they are very helpful in this type of question.