Question

How do you solve and graph the compound inequality $2x-6<-14$ or $2x+3<1$?

Answer 1

To solve the compound inequality first we separately solve both in equations. Then we will obtain two solutions by solving both equations. Then we plot a graph for each solution. The intersection of both the solutions is the required solution of the given system of equations.

Complete step-by-step solution:
We have been given a system of inequality equations $2x-6<-14$ or $2x+3<1$.
We have to solve and graph the given compound inequality.
First let us consider the equation $2x-6<-14$.
To solve the given equation first we will keep the variable term at the LHS of inequality and shift constant terms at the RHS. Then we will get
$\Rightarrow 2x<-14+6$
Now, simplifying the above obtained equation we will get
$\begin{aligned} & \Rightarrow 2x<-8 \\\ & \Rightarrow x<\dfrac{-8}{2} \\\ & \Rightarrow x<-4 \\\ \end{aligned}$
Now, let us consider the equation $2x+3<1$.
To solve the given equation first we will keep the variable term at the LHS of inequality and shift constant terms at the RHS. Then we will get
$\Rightarrow 2x<1-3$
Now, simplifying the above obtained equation we will get
$\begin{aligned} & \Rightarrow 2x<-2 \\\ & \Rightarrow x<\dfrac{-2}{2} \\\ & \Rightarrow x<-1 \\\ \end{aligned}$
Now, let us plot a graph for $x<-4$ and $x<-1$ then we will get

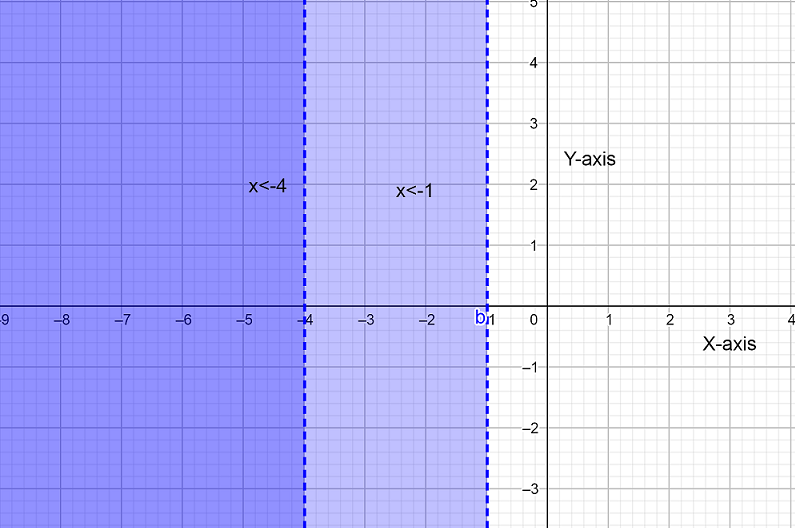
By observing the above graph we reach the conclusion that $x<-4$ is the common solution for both the inequality.
Hence $x <-4$ is the solution of given compound inequality.

Note: The point to be noted is that if we didn’t find any common intersection area by plotting the graph of solutions of two inequalities then there is no solution of the system of linear inequalities. If the equations have “or” then we need to combine two solutions and if the equations have “and” then the solution is where the two graphs overlap.