Question
Question: How do you solve \(4{\sin ^2}x + 1 = - 4\sin x\)?...
How do you solve 4sin2x+1=−4sinx?
Solution
First, we have to make the right side of the equation to be 0. Then, factor the left side of the equation. Next, substitute u for all occurrences of sinxand factor using the perfect square rule. Next, replace all occurrences of u with sinx and replace the left side with the factored expression. Next, set (2sinx+1) equal to 0 and solve for x using trigonometric properties. Then, we will get all solutions of the given equation.
Formula used:
Perfect square trinomial rule: 1) a2+2ab+b2=(a+b)2
2) sin6π=21
3) sin(π+x)=−sinx
4) sin(2π−x)=−sinx
Complete step by step solution:
Given equation: 4sin2x+1=−4sinx
We have to find all possible values of x satisfying a given equation.
First, we have to make the right side of the equation to be 0.
So, adding 4sinx to both sides of the given equation
4sin2x+4sinx+1=0
We have to factor the left side of the equation.
So, first put u=sinx, i.e., substitute u for all occurrences of sinx.
⇒4u2+4u+1
Now, we have to factor using the perfect square rule.
So, rewrite 4u2 as (2u)2.
⇒(2u)2+4u+1
Now, rewrite 1 as 12.
⇒(2u)2+4u+12
Now, we have to check the middle term by multiplying 2ab and compare this result with the middle term in the original expression.
2ab=2⋅(2u)⋅1
Simplifying this, we get
2ab=4u
Now, we have to factor using the perfect square trinomial rule a2+2ab+b2=(a+b)2, where a=2u and b=1.
⇒(2u+1)2
Now, replace all occurrences of u with sinx.
⇒(2sinx+1)2
Now, replace the left side with the factored expression.
⇒(2sinx+1)2=0
Now, set (2sinx+1) equal to 0 and solve for sinx.
Now, set the factor equal to 0.
⇒2sinx+1=0
Now, subtract 1 to both sides of the equation.
⇒2sinx=−1
Now, divide each term by 2 and simplify.
⇒sinx=−21…(i)
Now, using the property sin(π+x)=−sinx and sin6π=21 in equation (i).
⇒sinx=−sin6π
⇒sinx=sin(π+6π)
⇒x=67π
Now, using the property sin(2π−x)=−sinx and sin6π=21 in equation (i).
⇒sinx=−sin6π
⇒sinx=sin(2π−6π)
⇒x=611π
Since, the period of the sinx function is 2π so values will repeat every 2π radians in both directions.
x=67π+2nπ,611π+2nπ, for any integer n.
Final solution: Hence, x=67π+2nπ,611π+2nπ, for any integer nare solutions of the given equation.
Note:
In the above question, we can find the solutions of a given equation by plotting the equation, 4sin2x+1=−4sinx on graph paper and determine all its solutions.
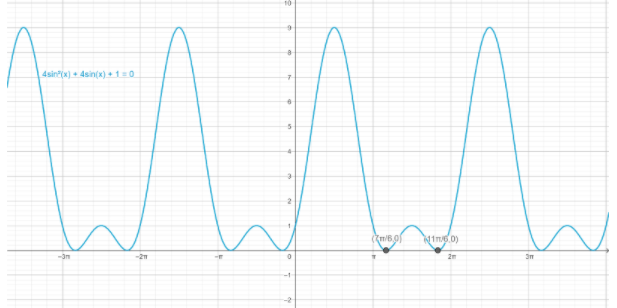
From the graph paper, we can see that x=67π and x=611π are solution of given equation, and solution repeat every 2π radians in both directions.
So, these will be the solutions of the given equation.
Final solution: Hence, x=67π+2nπ,611π+2nπ, for any integer n are solutions of the given equation.
