Question
Question: How do you solve \(3{\tan ^2}x = 1\) ?...
How do you solve 3tan2x=1 ?
Solution
Divide both the sides with 3 to remove the constant part from the left hand side and isolate the trigonometric function. Then we take the square root of both the sides to find the value of tanx. Then once we know the value of tanx, we can divide both sides of the equation to find the value of angle x and thus get our required answer.
Complete step-by-step solution:
The given expression is: 3tan2x=1.
Now, we need to isolate our trigonometric function tan2x , in order to do so, we divide both the sides of the expression with 3 so that our left hand side of the expression becomes free of any constant:
Therefore,
⇒tan2x=31
Now we take out the square –root on both the sides of the expression:
tan2x=31
⇒tanx=±31 , thus we have two roots of tanx : +31,−31 , because on taking out the square root of non-square numbers we get two values: positive and negative.
Taking the positive value of root:
tanx=31
Now, we know that tanθ=31=30∘
Here x represents θ , therefore tanx=31=30∘
Therefore x=30∘ In the first quadrant. x can also be +31 in the third quadrant as all functions of tan are positive here as shown in the picture below:
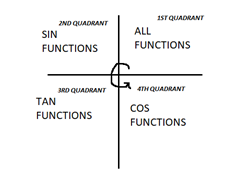
Therefore tanx=+31 when x=30∘,(180∘+30∘)=30∘,210∘
Taking the negative value of root:
tanx=−31
Now, the value of tanx can be negative in the second and fourth quadrant.
Therefore the values of x in the second quadrant can be (180−30∘)=150∘ where 180∘ represent a complete transition from the First quadrant to the third quadrant.
In the fourth quadrant the value of x=360−30∘, where 360∘ represents one complete circle around all the quadrants starting from the first quadrant.
Therefore the values of x are: 30∘,150∘,210∘,330∘
Note: Some trigonometric values related to tan that needs to be remember are:
tan30∘=31
tan45∘=1
tan60∘=3
tan90∘=∞
