Question

How do you solve $|2x+1|=5$ ?

Answer 1

Here, we need to find the value of ‘x’. In case of absolute value or modulus, we have to find a negative and a non-negative value of ‘x’. As we already know that modulus give us both positive and negative solutions.
|x|=\left\\{ \begin{aligned} & x,x\ge 0 \\\ & -x,x<0 \\\ \end{aligned} \right.
This is the basic function of absolute value or modulus.

Complete step by step answer:
Now, let’s solve the question.
First, we need to write the equation as given in the question:
$\Rightarrow |2x+1|=5$
Firstly, we will solve for the positive value of ‘x’ by removing the modulus sign. Let’s see how this will happen.
$\Rightarrow 2x+1=5$
Now, find the value of x by solving the equation:
$\begin{aligned} & \Rightarrow 2x=5-1 \\\ & \Rightarrow 2x=4 \\\ & \Rightarrow x=\dfrac{4}{2} \\\ \end{aligned}$
After cancellation:
$\therefore x=2$
Now, we will solve for the negative value of ‘x’ by removing the modulus sign. On removing the modulus, the negative sign will come with 5. Let’s see how!
$\Rightarrow |2x+1|=5$
$\Rightarrow 2x+1=-5$
Now, find the value of x by solving the equation:
$\begin{aligned} & \Rightarrow 2x=-5-1 \\\ & \Rightarrow 2x=-6 \\\ & \Rightarrow x=\dfrac{-6}{2} \\\ \end{aligned}$
After cancellation:
$\therefore x=-3$

**Finally, we have got the positive and negative value of x: 2, -3.

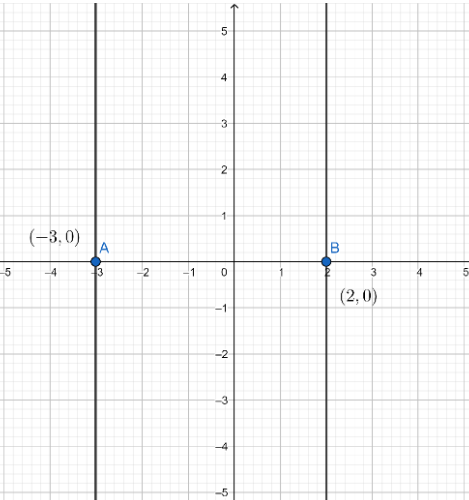
We can even see graphically that on finding the absolute value or modulus of the given equation we got the same values on plotting the equation on graph. **

Note: It is necessary to find both positive and negative values for modulus. If you find a single value for ‘x’, then the question will remain incomplete. To check the solution, the best way is to plot the graph of it. Do remember that if the value of ‘x’ comes out to be 0 then it will be considered as a positive value.