Question

How do you sketch the region enclosed by the given curves and decide whether to integrate with respect with respect to $x$ or $y$, then find the area of the region of $2y = 3x$, $y = 5$ and $2y + 1x = 4$?

Answer 1

Here we will write all the straight line graphs in standard form. From there, we will find the values of the intercepts of both the lines. Then we will find the points of intersection of all the graphs in order to determine the limits of the integration. Then we will split this area up into two parts and hence we will use 2 definite integrals. After simplifying the limits, we will get the required value.

Complete step by step solution:
Here we will write all the straight line graphs in standard form. The first equation of the line is $2y = 3x$.
We can write the equation by dividing both sides by 2 as
$\dfrac{{2y}}{2} = \dfrac{{3x}}{2}$
$\Rightarrow y = \dfrac{3}{2}x$ …………… $\left( 1 \right)$
We know that the slope intercept form of an equation is given by $y = mx + b$.
Here, $m$ is the slope of the line and $b$ is the $y$ intercept of the straight line.
Now, we will compare this equation with the given equation.
Slope in this case is $\dfrac{3}{2}$ and $y$ intercept is equal to 0.
Now, we will find the $x$ intercepts by putting the value of $y$ as zero.
$0 = \dfrac{3}{2}x$
On further simplification, we get
$\begin{array}{l} \Rightarrow 0 = x\\\ \Rightarrow x = 0\end{array}$
Therefore, the $x$ intercept is equal to 0.
Therefore, the $x$ intercept of the straight line $2y = 3x$ is equal to 0, $y$ intercept is equal to 0 and slope is equal to $\dfrac{3}{2}$.
The second equation is $2y + 1x = 4$.
Now, we will write it in standard form.
We will first subtract the term $x$ from both sides.
$\begin{array}{l}2y + x - x = 4 - x\\\ \Rightarrow 2y = - x + 4\end{array}$
Now, we will divide both sides by 2.
$\Rightarrow \dfrac{{2y}}{2} = \dfrac{{ - x}}{2} + \dfrac{4}{2}$
$\Rightarrow y = \dfrac{{ - 1}}{2}x + 2$ …………. $\left( 2 \right)$
We know that this is an equation of straight line and the given equation is written in the slope intercept form.
We know that the slope intercept form of an equation is given by $y = mx + b$.
Here, $m$ is the slope of the line and $b$ is the $y$ intercept of the line.
Now, we will compare this equation with the given equation.
Slope in this case is $\dfrac{{ - 1}}{2}$ and the$y$ intercept is equal to 2.
Now, we will find the $x$ intercepts by putting the value of $y$ as zero.
$0 = \dfrac{{ - 1}}{2}x + 2$
Now, we will subtract 2 from both sides.
$\begin{array}{l} \Rightarrow 0 - 2 = \dfrac{{ - 1}}{2}x + 2 - 2\\\ \Rightarrow - 2 = \dfrac{{ - 1}}{2}x\end{array}$
Now, multiplying both sides by $- 2$, we get
$\Rightarrow - 2 \times - 2 = \dfrac{{ - 1}}{2}x \times - 2$
On further simplification, we get
$\begin{array}{l} \Rightarrow 4 = x\\\ \Rightarrow x = 4\end{array}$
Therefore, the $x$ intercept is equal to 4.
Therefore, the $x$ intercept of the straight line $2y + 1x = 4$ is equal to 4, $y$ intercept is equal to 2 and slope is equal to$\dfrac{{ - 1}}{2}$.
Now, we will calculate the point of intersection of these two lines.
Substituting the value of $y$ from equation $\left( 1 \right)$ in equation $\left( 2 \right)$, we get
$\dfrac{3}{2}x = \dfrac{{ - 1}}{2}x + 2$
Adding the term $\dfrac{1}{2}x$ to both sides, we get
$\begin{array}{l} \Rightarrow \dfrac{3}{2}x + \dfrac{1}{2}x = \dfrac{{ - 1}}{2}x + 2 + \dfrac{1}{2}x\\\ \Rightarrow \dfrac{4}{2}x = 2\end{array}$
On further simplification, we get
$\Rightarrow 2x = 2$
Dividing both sides by 2, we get
$\begin{array}{l} \Rightarrow \dfrac{{2x}}{2} = \dfrac{2}{2}\\\ \Rightarrow x = 1\end{array}$
Now, we will substitute the obtained value of variable $x$ in equation $\left( 1 \right)$. Therefore, we get
$y = \dfrac{3}{2} \times 1 = \dfrac{3}{2}$
Hence, the point of intersection of these two lines is $\left( {1,\dfrac{3}{2}} \right)$.
Now, we will find the point intersection of the line of equation $y = \dfrac{3}{2}x$ with the line $y = 5$ by putting the value $y = 5$ in the equation of the line.
$5 = \dfrac{3}{2}x$
Dividing both sides by $\dfrac{3}{2}$, we get
$\begin{array}{l} \Rightarrow \dfrac{5}{{\dfrac{3}{2}}} = \dfrac{{\dfrac{3}{2}x}}{{\dfrac{3}{2}}}\\\ \Rightarrow \dfrac{{10}}{3} = x\end{array}$
Hence, the intersection point of $y = \dfrac{3}{2}x$ with the line $y = 5$ is equal to $\left( {\dfrac{{10}}{3},5} \right)$.
Now, we will find the point intersection of line of equation $y = \dfrac{{ - 1}}{2}x + 2$ with the line $y = 5$ by putting the value $y = 5$ in equation of the line.
$\Rightarrow 5 = - \dfrac{1}{2}x + 2$
Now, we will subtract 2 from sides.
$\begin{array}{l} \Rightarrow 5 - 2 = - \dfrac{1}{2}x + 2 - 2\\\ \Rightarrow 3 = - \dfrac{1}{2}x\end{array}$
Multiplying both sides by $- 2$, we get
$\begin{array}{l} \Rightarrow 3 \times - 2 = - \dfrac{1}{2}x \times - 2\\\ \Rightarrow - 6 = x\\\ \Rightarrow x = - 6\end{array}$
Hence, the intersection point of $y = \dfrac{{ - 1}}{2}x + 2$ with the line $y = 5$ is equal to $\left( { - 6,5} \right)$.
Now, we will draw the graph using the slope and the intercepts and the intersection points.

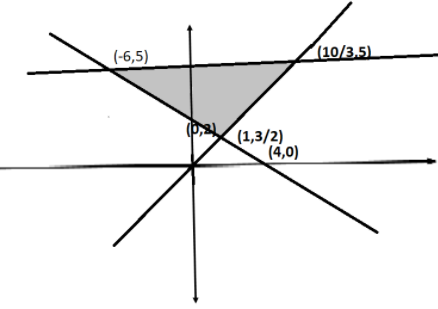
Now, we will find the area of the shaded area using the integration.
Area of the shaded region $= \int\limits_{ - 6}^1 {\left[ {5 - \left( {\dfrac{{ - 1}}{2}x + 2} \right)} \right]} + \int\limits_1^{\dfrac{{10}}{3}} {\left[ {5 - \dfrac{3}{2}x} \right]}$
Now, we will further simplify the terms.
$\Rightarrow$ Area of the shaded region $= \int\limits_{ - 6}^1 {\left[ {3 - \dfrac{1}{2}x} \right]} + \int\limits_1^{\dfrac{{10}}{3}} {\left[ {5 - \dfrac{3}{2}x} \right]}$
Integrating each term, we get
$\Rightarrow$Area of the shaded region $= \left[ {3x - \dfrac{{{x^2}}}{4}} \right]_{ - 6}^1 + \left[ {5x - \dfrac{{3{x^2}}}{4}} \right]_1^{\dfrac{{10}}{3}}$
Applying the limits, we get
$\Rightarrow$ Area of shaded region $= \left[ {3 \times 1 - \dfrac{{{1^2}}}{4} - \left( {3 \times - 6 - \dfrac{{{{\left( { - 6} \right)}^2}}}{4}} \right)} \right]_{ - 6}^1 + \left[ {5 \times \dfrac{{10}}{3} - \dfrac{{3{{\left( {\dfrac{{10}}{3}} \right)}^2}}}{4} - \left( {5 \times 1 - \dfrac{{3 \times {1^2}}}{4}} \right)} \right]$
On further simplifying the terms, we get
$\Rightarrow$ Area of the shaded region $= \left[ {3 - \dfrac{1}{4} - \left( { - 18 - 9} \right)} \right] + \left[ {\dfrac{{50}}{3} - \dfrac{{25}}{3} - \left( {5 - \dfrac{3}{4}} \right)} \right]$
On subtracting and adding the terms, we get
$\Rightarrow$ Area of the shaded region $= \dfrac{{49}}{3}$ sq. units
Hence, the area bounded by the lines is equal to $\dfrac{{49}}{3}$ sq. units.

Note:
Here we have obtained the required graph of the given equation. Here we have obtained the value of the slope of the line using the slope intercept form of the equation. Slope of a line is defined as the value which measures the steepness of the line or the inclination of the line with the $x$ axis. Integration is defined as the summation of all the discrete data. Integration is used to find the area bounded by a curve of a function.