Question

How do you sketch the graph $y={{x}^{4}}-2{{x}^{3}}+2x$ using the first and second derivatives?

Answer 1

We find the slope of the given function $f\left( x \right)=y={{x}^{4}}-2{{x}^{3}}+2x$ to find the extremum points. We equate it with 0. Extremum points in a curve have slope value 0. We solve the quadratic solution to find the X-axis intersects and the points.

Complete step by step answer:
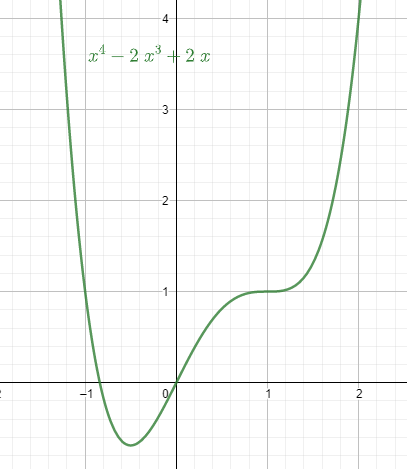
We need to find the relative extrema of the function $f\left( x \right)={{x}^{4}}-2{{x}^{3}}+2x$.
To find the extremum points we need to find the slope of the function and also the value of the point where the slope will be 0.
Extremum points in a curve have slope value 0.
The slope of the function $f\left( x \right)={{x}^{4}}-2{{x}^{3}}+2x$ can be found from the derivative of the function ${{f}^{'}}\left( x \right)=\dfrac{d}{dx}\left[ f\left( x \right) \right]$.
We know that the differentiation form for ${{n}^{th}}$ power of $x$ is $\dfrac{d}{dx}\left[ {{x}^{n}} \right]=n{{x}^{n-1}}$.
$\begin{aligned} & f\left( x \right)={{x}^{4}}-2{{x}^{3}}+2x \\\ & \Rightarrow {{f}^{'}}\left( x \right)=\dfrac{d}{dx}\left[ f\left( x \right) \right]=4{{x}^{3}}-6{{x}^{2}}+2 \\\ \end{aligned}$
To find the $x$ coordinates of the extremum points we take $4{{x}^{3}}-6{{x}^{2}}+2=0$.
So, $4{{x}^{3}}-6{{x}^{2}}+2={{\left( x-1 \right)}^{2}}\left( 4x+2 \right)$.
We put the values and get $x$ as $x=1,-\dfrac{1}{2}$.
We also can find which point is maxima and minima by finding ${{f}^{''}}\left( x \right)=\dfrac{d}{dx}\left[ {{f}^{'}}\left( x \right) \right]$. If for $x=a,b$, we find ${{f}^{''}}\left( x \right)$ being negative value then the point is maxima and ${{f}^{''}}\left( x \right)$ being positive value then the point is minima.
For ${{f}^{'}}\left( x \right)=4{{x}^{3}}-6{{x}^{2}}+2$, we get ${{f}^{''}}\left( x \right)=12{{x}^{2}}-12x$.
At $x=1$, ${{f}^{''}}\left( 1 \right)=0$. The point is neither maxima or minima.
At $x=-\dfrac{1}{2}$, ${{f}^{''}}\left( -\dfrac{1}{2} \right)=9>0$. The point $x=-\dfrac{1}{2}$ is minima.
Therefore, from the value of the $x$ coordinates of the extremum points, we find their $y$ coordinates.
For $x=-\dfrac{1}{2}$, the value of $y=f\left( -\dfrac{1}{2} \right)={{\left( -\dfrac{1}{2} \right)}^{4}}-2{{\left( -\dfrac{1}{2} \right)}^{3}}+2\left( -\dfrac{1}{2} \right)=-\dfrac{11}{16}$.

Note:
We also find the X-axis intersects and the points where ${{x}^{4}}-2{{x}^{3}}+2x=0$.
This gives $x=0$ as the only integer root. The other real root is fraction
The curve is open on the maximum side.