Question

How do you sketch the graph of $y = {x^2} - 5$ and describe the transformation?

Answer 1

The basic equation of parabola is $y = a{x^2} + c$, in which the vertical movement along a parabola’s line of symmetry is called a vertical shift. A vertical shift is when the graph literally moves vertically, up or down. As the given equation is a quadratic equation, the graph of a quadratic function is represented using a parabola. Vertex of a quadratic equation is its minimum or lowest point if the parabola is opening upwards or its highest or maximum point if it opens downwards.

Complete step by step solution:
Given,
$y = {x^2} - 5$
If you know the graph of a function $y = f\left( x \right)$, then you can have four kind of transformations: the most general expression is:
$Af\left( {wx + h} \right) + v$
Where:
\to $$$$Amultiplies the whole function, thus stretching it vertically (expansion if $\left| A \right| > 1$, contraction otherwise)
\to $$$$wmultiplies the input variable, thus stretching it horizontally (expansion if $\left| w \right| > 1$, contraction otherwise)
$\to$h and v are, respectively, horizontal and vertical translations.
In this given function, starting from $f\left( x \right) = {x^2}$, you have $A = 1$and $w = 1$. Being multiplicative factors, they have non-effect.
Moreover, $h = 0$. Being ad additive factor, it has non-effect.
Finally, you have $v = - 5$. This means that, if you start from the "standard" parabola $f\left( x \right) = {x^2}$, to describe the transformation going on the graph of $f\left( x \right) = {x^2} - 5$ is the same, just translated 5 units down.
The graph is shown as:

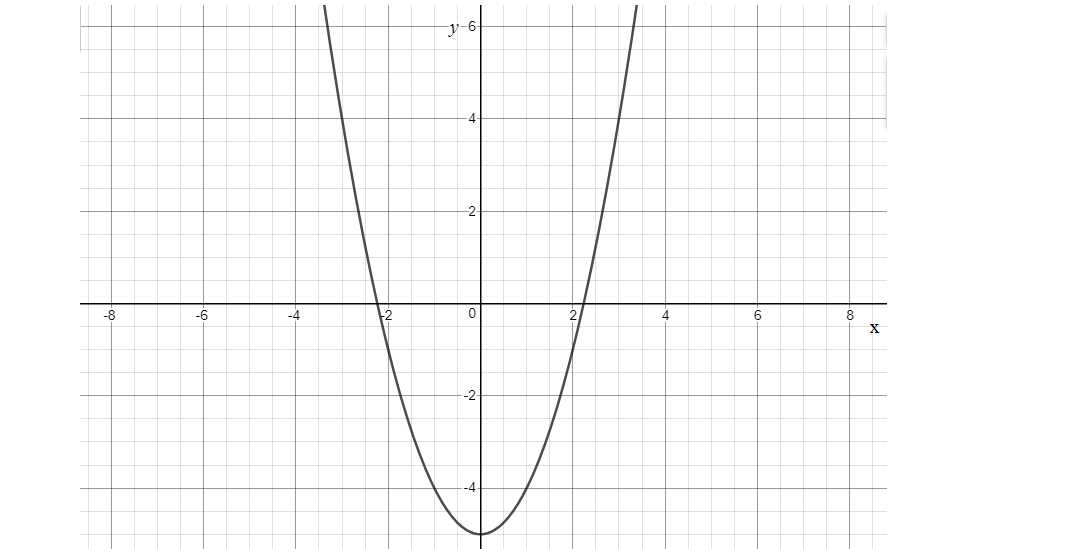
Note: We know that the basic equation of parabola is $y = a{x^2} + c$, here given function we have a=1, if a is positive the parabola opens upwards as a is greater than 1, the parabola is narrow about its line of symmetry. The movement is all based on the y-value of the graph. The y-axis of a coordinate plane is the vertical axis. When a function shifts vertically, the y-value changes. Adding or subtracting a positive constant k to $f\left( x \right)$ is called a vertical shift. Adding or subtracting a positive constant h to x is called a horizontal shift.