Question

How do you sketch the graph of $y = {\left( {x - 3} \right)^2}$ and describe the transformation?

Answer 1

Here we have to show the graphical representation of $y = {\left( {x - 3} \right)^2}$ . To do so, our first approach is to find different values of $y$ for the different values of $x$ . Then, we will plot the obtained points on a graph. Therefore we can sketch the graph of $y = {\left( {x - 3} \right)^2}$ by joining all the points with a curved line. Also, in the given equation $y = {\left( {x - 3} \right)^2}$ , the R.H.S. is whole squared which means that $y$ will always be a non-negative number. Therefore, for all values of $x$ , the graph will lie above the x-axis, i.e. in the first and second quadrant.

Complete step by step answer:
Given equation is $y = {\left( {x - 3} \right)^2}$ .
Now we have to find different coordinates which satisfy the equation, i.e. those points which lie on the above curve.
Hence, we will put random values for $x$ and find the related value of $y$ for that $x$ or vice-versa.
Now, putting the value $x = 0$ in the equation $y = {\left( {x - 3} \right)^2}$ ,
We get,
$y = {\left( {0 - 3} \right)^2}$
$y = {\left( { - 3} \right)^2}$
Solving the R.H.S., we get
$y = 9$
Therefore, $y = 9$ for $x = 0$ .
Similarly, putting the value $y = 0$ in $y = {\left( {x - 3} \right)^2}$
We get,
$0 = {\left( {x - 3} \right)^2}$
Taking square root of both sides,
$x - 3 = 0$
Adding 3 both sides, we get
$x = 3$
Therefore, $x = 3$ for $y = 0$
Again, putting the value $x = 4$ in the equation $y = {\left( {x - 3} \right)^2}$
We get,
$y = {\left( {4 - 3} \right)^2}$
Solving the R.H.S., we get
$y = {\left( 1 \right)^2}$
or
$y = 1$
Therefore, $y = 1$ for $x = 4$
Now the three obtained points are:

$x$	$0$	$3$	$4$
$y$	$9$	$0$	$1$

Therefore, the three coordinates that lie on the curve $y = {\left( {x - 3} \right)^2}$ are $\left( {0,9} \right)$ , $\left( {3,0} \right)$ and $\left( {4,1} \right)$ .
Plotting these points on a graph and then extending the curve after joining all the points gives us the graph of $y = {\left( {x - 3} \right)^2}$ .
The obtained graph is shown below:

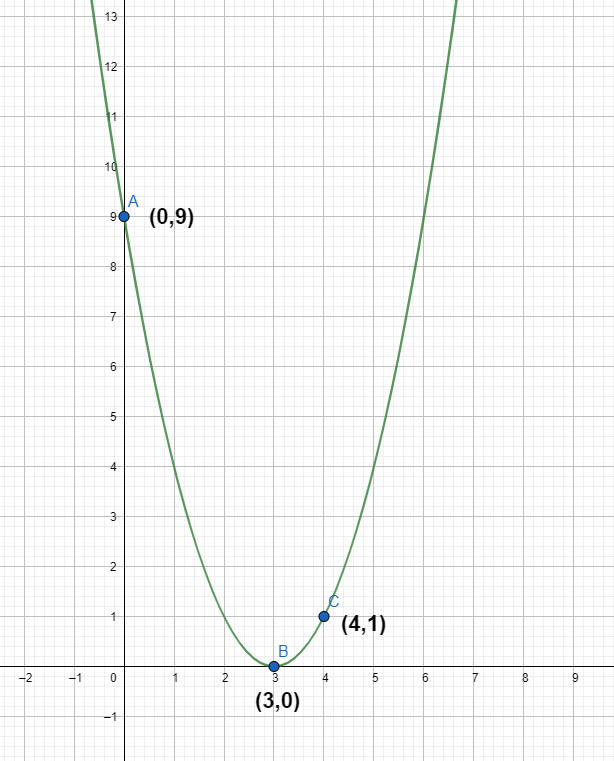
That is the required graphical representation of the equation $y = {\left( {x - 3} \right)^2}$ .
When the equation is given in its particular form as $y = {\left( {x - a} \right)^2}$ , then the curve is shifted by $a$ units on the x-axis. In that case, the point of contact of the curve and the x-axis is $\left( {a,0} \right)$ . For example, in the above equation $y = {\left( {x - 3} \right)^2}$ , the curve was shifted by $3$ units on the x-axis.

Note:
The standard form of such curves is $y = {x^2}$ . That curve also looks similar to the curve in the above graph but the curve touches the x-axis at the origin $\left( {0,0} \right)$ . The given graph depicts an upward facing parabola touching the x axis at $\left( {3,0} \right)$.