Question

How do you sketch the graph of $y=-{{\left( x+2 \right)}^{2}}-2$ and describe the transformation?

Answer 1

These types of problems are pretty straight forward and are very easy to solve. The given problem is a simple demonstration of coordinate geometry of subtopic parabola. For plotting the graphs, we require a knowledge of graph theory and functions as well. For sums like these we first of all need to rearrange the equation in such a way that it represents one of the general equations of a parabola. Some of the general equations of the parabola are as follows.

Equation	Vertex	Foci
${{y}^{2}}=4ax$	$\left( 0,0 \right)$	$\left( a,0 \right)$
${{y}^{2}}=-4ax$	$\left( 0,0 \right)$	$\left( -a,0 \right)$
${{x}^{2}}=4by$	$\left( 0,0 \right)$	$\left( 0,b \right)$
${{x}^{2}}=-4by$	$\left( 0,0 \right)$	$\left( 0,-b \right)$

Complete step by step solution:
Now we start off with the solution of the problem by writing that,
We first of all rearrange our given problem as,
$y+2=-{{\left( x+2 \right)}^{2}}$
Now, we make a transformation or in other words we can say that we shift the origin of the given function to some other point in such a way that the problem equation becomes similar to that of one of the general equations.
For the transformation, we can write,
$Y=y+2,X=x+2$
Or in other words we can say that we shift the origin of the equation to the point $\left( -2,-2 \right)$ . The equation hence transforms to,
${{X}^{2}}=-Y$
Now, we can very clearly observe that the above equation looks similar to that of the equation ${{x}^{2}}=-4by$.
Thus we plot our graph having a vertex of $\left( -2,-2 \right)$ instead of $\left( 0,0 \right)$ . The nature of the graph will be the same as well as its curvature will also be same.

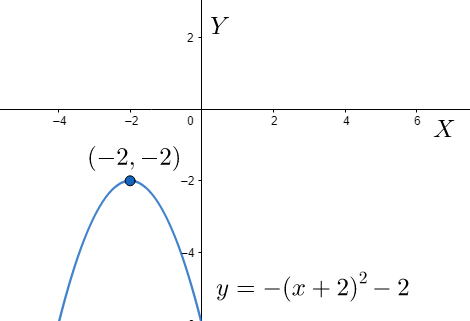
Note: For problems like these we need to be very thorough and fluent in functions as well as graph theory. While transforming an equation or shifting its origin we need to be very careful because, once we shift the origin of the function, we must also revert back to the original coordinate system after all our calculations have been done. We should also remember that when we transform or shift the origin form $\left( 0,0 \right)$ to some point $\left( a,b \right)$ , then all the other points also gets shifted by $\left( a,b \right)$ .