Question

How do you sketch the graph of $y=-5{{x}^{2}}$ and describe the transformation?

Answer 1

Now we know that the graph of quadratic function is a parabola. If a > 0 then the parabola is upward facing and if a < then the parabola is downward facing. Now we will find the roots and intercept of the function and determine its vertex using first derivative test. Hence we get the information to draw the graph of the function.

Complete step-by-step answer:
Now consider the given function $y=-5{{x}^{2}}$ .
The function is a quadratic function of the form $a{{x}^{2}}+bx+c$ where a = - 5, b = c = 0.
We know that the graph of the quadratic functions are always parabolic.
Now we know that if a < 0 then the graph of the function is concave down.
Since here we have a < 0 we can say the given function is a parabolic function with its graph as concave down.
Now on factorizing the given equation we get, $y=x\left( -5x \right)$ Now y = 0 only if x = 0. Hence the function has root at x = 0. Since the roots are repeating roots we can say that the function will touch the x axis only once at x = 0.
Now we know that at x = 0 $y=-5{{x}^{2}}=0$ . Hence the y intercept of the function is also zero.
Now let us check the first derivative of the function.
$y'=-10x$ .
Now we can see that the derivative is negative for x > 0 and positive form x < 0.
Hence the function is increasing for x < 0 and decreasing for x > 0.
Also we know that $f'\left( x \right)=0$ gives the condition for extremum.
$\begin{aligned} & \Rightarrow -10x=0 \\\ & \Rightarrow x=0 \\\ \end{aligned}$
Hence we have an extremum at x = 0.
Now since the parabola is concave down we can say that the extremum is maxima of the function.
Hence the function starts from $-\infty$ and increase till it reaches the point $\left( 0,0 \right)$ . then it reach the vertex and decrease and again tend to $-\infty$ . Hence the whole function is below x axis.
Hence the graph of the function will look like,

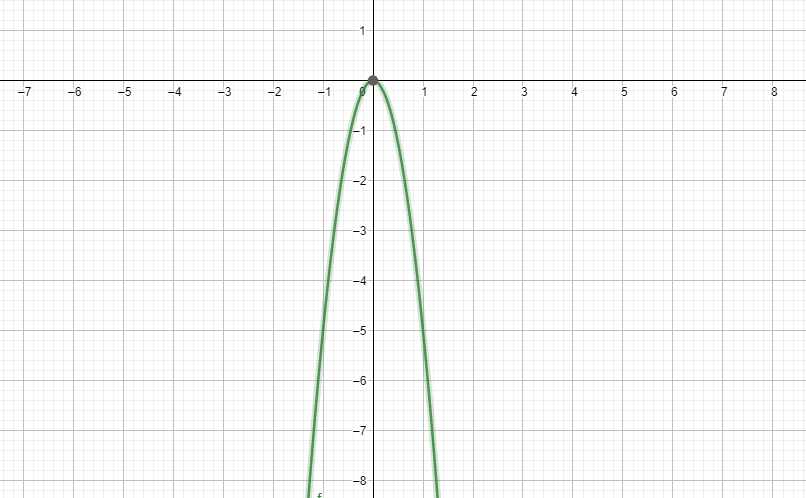
Note: Now note that if a > 0 then the parabola is upward facing parabola. The roots of the equation of the form $a{{x}^{2}}+bx+c$ is given by $\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$ . Also the vertex of parabola is given by $\left( \dfrac{-b}{2a},f\left( \dfrac{-b}{2a} \right) \right)$ .