Question

How do you sketch the graph of $y={{(2x)}^{2}}$ and describe the transformation?

Answer 1

For solving this problem, first we have to understand the transformation in graphs and then we will find the parent function for a given function and then sketch the graph of both the functions and compare both of them on different aspects and we will get the transformations in both the graphs.

Complete step-by-step solution:
As we are given in the question $y={{(2x)}^{2}}$
The parent function can be defined as the simplest form of the type of function given.
So, the parent function for $y={{(2x)}^{2}}$ be
$y={{x}^{2}}$
Now for better explanation, let us assume that
$f(x)=y={{x}^{2}}$
$\Rightarrow f(x)={{x}^{2}}$
And
$g(x)=y={{(2x)}^{2}}$
$\Rightarrow g(x)=4{{x}^{2}}$
Now, we will describe the transformation from the parent function to the given function (I.e. from $f(x)$ to $g(x)$ )
Let’s graph the both function the parent function and the given function:

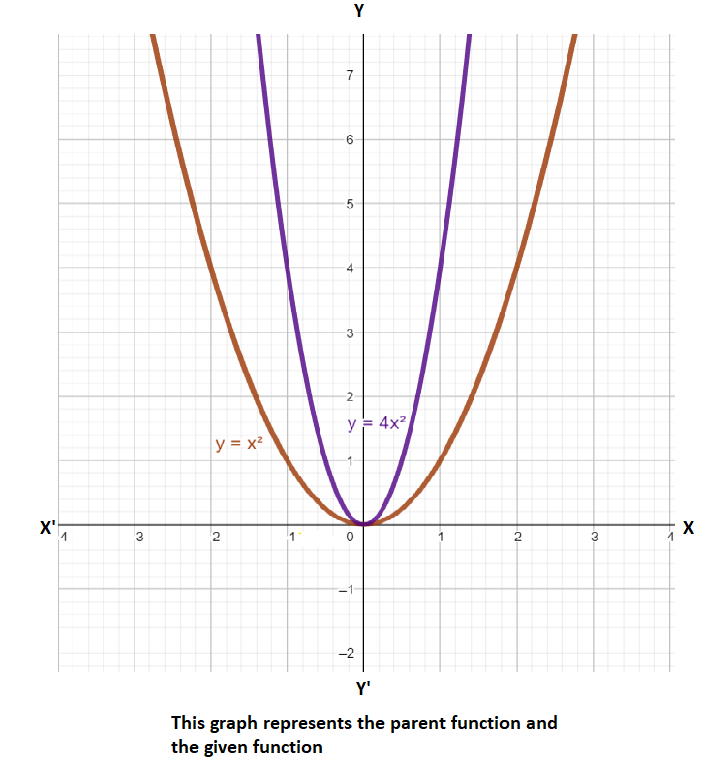
First let’s discuss the horizontal shift:
The horizontal shift depends on the value of $h$ .The horizontal shift is described as:
1. $g(x)=f(x+h)$ .In this condition the graph is shifted to the left $h$ units.
2. $g(x)=f(x-h)$ .In this condition the graph is shifted to the right $h$ units.
3. In case when $h=0$ , it means that the graph is not shifted to the left or right.
So, now as from our given function and parent function we can say that the transformation in horizontal shift is none (i.e. Horizontal shift: None)
The vertical shift depends on the value of $k$ .The vertical shift is described as:
1. $g(x)=f(x)+k$ .In this condition the graph is shifted up $k$ units.
2. $g(x)=f(x)-k$ .In this condition the graph is shifted down $k$ units.
3. In case when $k=0$ , it means that the graph is shifted neither up nor down.
Now when we will compare the parent function and the given function, there is no transformation in the vertical shift (i.e. Vertical shift: None)
As from the graph we can observe that there is no reflection about the $x$ axis and the $y$ axis.
Now, we will discuss the transformation in compressing and stretching of the graph.
As, parent function: $y={{x}^{2}}$
And the given function: $y={{(2x)}^{2}}=4{{x}^{2}}$
As in this we can observe that $4>1$ , Therefore we can say that the graph is stretched.
List of the transformations:
Horizontal shift: None
Vertical Shift: None
Reflection about the $x$ axis: None
Reflection about the $y$ axis: None
Vertical compression or stretch: Stretched

Note: Identifying transformations allows us to quickly sketch the graph of functions. By seeing some expression we cannot make a graph directly therefore we study transformation of graphs which is very useful as we can make graphs of such expressions from the basic function we already know.