Question

How do you sketch the graph of $y = 0.5{\left( {x - 2} \right)^2} - 2$ and describe the transformation?

Answer 1

In this question compare the given function to the related parental function and compare the terms, and check horizontal, vertical shifts and the reflection of the graph with the given values of $h,a,k$ in the function.
The horizontal shift depends on the value of $h$, the vertical shift depends on the value of $k$, and the sign of $a$ describes the reflection across the $x$-axis.

Complete step-by-step solution:
Given function $y = 0.5{\left( {x - 2} \right)^2} - 2$,
Since the equation is in the form of $y = a{\left( {x - h} \right)^2} + k$, the graph's turning point shifts $2$ units to the right, and $2$ units down. Therefore, the turning point is $\left( {2, - 2} \right)$. The next step is to find the intercepts.
Here , $h = 2$,$a = \dfrac{1}{2}$ and $k = - 2$.
The horizontal shift depends on the value of $h$. The horizontal shift is described as:
$g\left( x \right) = f\left( {x + h} \right)$- The graph is shifted to the left $h$ units.
$g\left( x \right) = f\left( {x - h} \right)$- The graph is shifted to the right $h$ units.
Horizontal Shift: Right $2$ Units.
The vertical shift depends on the value of $k$. The vertical shift is described as:
$g\left( x \right) = f\left( x \right) + k$ - The graph is shifted up $k$ units.
$g\left( x \right) = f\left( x \right) - k$ - The graph is shifted down $k$ units.
Vertical Shift: Down $2$ Units.
The sign of $a$ describes the reflection across the $x$-axis. $- a$ means the graph is reflected across the $x$-axis..
Reflection about the $x$-axis: None
The value of $a$ describes the vertical stretch or compression of the graph.
$a > 1$ is a vertical stretch (makes it narrower)
$0 < a < 1$ is a vertical compression (makes it wider)
Vertical Compression or Stretch: Compressed.
To find the transformation, compare the equation to the parent function and check to see if there is a horizontal or vertical shift, reflection about the $x$-axis or $y$-axis, and if there is a vertical stretch.
Now graph the function with the data we have, we get,

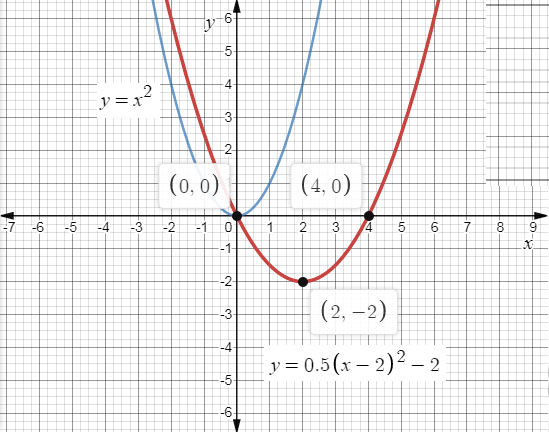
As you can see, the graph has shifted 2 units to the right and 2 units down compared to $y = {x^2}$. The graph is also wider than $y = {x^2}$. Since the value of $a$ in the equation is $\dfrac{1}{2}$.
Final Answer:
The graph for the function $y = 0.5{\left( {x - 2} \right)^2} - 2$ is,

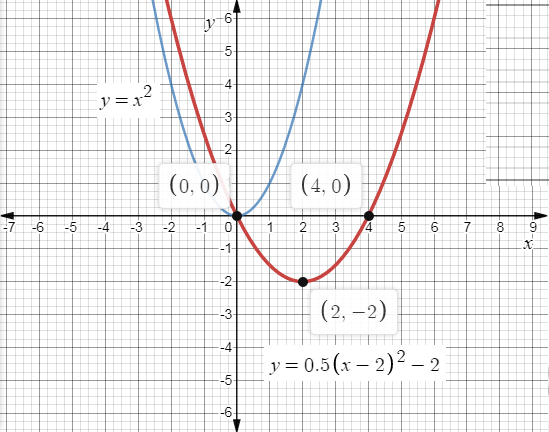
And Parent Function:$y = {x^2}$
Horizontal Shift: Right $2$Units
Vertical Shift: Down$2$Units
Reflection about the$x$-axis: None
Reflection about the $y$-axis: None
Vertical Compression or Stretch: Compressed.

Note: One definition of "to translate" is "to change from one place, state, form, or appearance to another". When we take a function and tweak its rule so that its graph is moved to another spot on the axis system, yet remains recognizably the same graph, we are said to be "translating" the function. Usually, translation involves only moving the graph around. Squeezing or stretching a graph is more of a "transformation" of the graph. But these two topics are usually taught at the same time, and usually under the same name. Just be aware that the topic of "function translation" often includes function transformation, and vice versa.